Piacszegmentalas

Piacszegmentálás

Szegmentum: a termék fogyasztása szempontjából releváns változók szerinti homogén csoportok.

Lehetséges szegmentálási változók: földrajzi, demográfiai, pszichográfiai (pl. életstílus - személyiség és demográfiai jellemzők alapj 626f51g án), magatartás (pl. termékhasználat, ismeret, attitűd).

A c statisztika két változó (X és Y) közti összefüggés statisztikai szignifikanciáját méri, segít meghatározni van-e szisztematikus kapcsolat a két változó között.

H₀ (null hipotézis) az, hogy nincs összefüggés két változó között.

H₁ (alternatív hipotézis) az, hogy van összefüggés két változó között (pl. a szegmentálási kritériumok és a piaci szegmensek között).

A null hipotézis tesztelési lépései:

a.     Felmérést készítünk egy reprezentatív mintán a két változó (X és Y) valóságos értékeiről. Az eredményeket kereszttáblába (kontingencia-táblába) tüntetjük fel, amely két vagy több változó gyakorisági eloszlásának összevonása egy táblázatba.

Ahol,

m, n - az X és Y változók száma

X_ij - az "i" szegmens nagysága a "j" szegmentálási kritérium alapján

X_j - az adott oszlop összege

K_i - az adott sor összege

X - a teljes mintanagyság

b.            Kiszámítjuk a cellák várt gyakoriságát (elméleti gyakoriságát amennyiben nincs korreláció a két változó között)  a következő képlettel:

f_ij = , i = 1,m ; j = 1,n

c.     Kiszámítjuk a c statisztika értékét a következő képlettel:

c_calc = 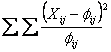, minden cellára

d.            Összehasonlítjuk a  c_tab értékét 95% valószínűséggel (p), az adott szabadságfokokkal (g) (a Fisher táblázat alapján) a kereszttáblából számított értékel c_calc

P = 0,95

A kereszttáblázathoz kapcsolódó c statisztika esetén, a szabadságfokok száma egyenlő a sorok száma mínusz egy, illetve az oszlopok száma mínusz egy

g = (m-1)(n-1)

Ha adott szabadságfok mellet a próbafüggvény számított értéke nagyobb, mint c - eloszlás kritikus értéke (c_calc ³ c_tab ), a null hipotézist (H₀) elutasítjuk, azaz a szegmentálási kritériumok szignifikánsak. Ellenkező esetben,  a szegmentálási kritériumok nem szignifikánsak.

e.     Abban az esetben ha a c statisztika teszt alapján a szegmentálási kritériumok szignifikánsaknak bizonyultak, következő lépésben elkészítjük a piaci szegmentum-fát. 

A szegmentálási változók fontossági sorrendjét a következő képlet alapján számítjuk ki: Max (c_calc c_tab