PORTFÓLIÓ MENEDZSMENT - EGYEDI ÉRTÉKPAPÍROK ÉRTÉKELÉSE

EGYEDI ÉRTÉKPAPÍROK ÉRTÉKELÉSE

Alapfogalmak

Tökéletes tökepiac, intertemporális allokáció, idöpreferencia, Fisher szeparáció, diszkontálás.

Bizonyosság, kockázat, bizonytalanság, kockázat-kerülés, hasznossági függvény, kilátáselmélet, biztonságos egyenértékes, gyengén, közepesen, erösen hatékony tökepiacok, véletlen bolyongás, fundamentális elemzés, technikai elemzés, aktív és passzív portfóliómenedzsment.

Szelvény, névérték, árfolyam, kamatszelvényes kötvény, zérókupon-kötvény, örökjáradék-kötvény, opciós tulajdonságú kötvények, kötvényárfolyam-konvergencia, lejárati hozam, lineáris interpoláció, normál hozamgörbe, inverz hozamgörbe, várakozások.

Duráció, Macaulay-féle duráció, volatilitás, immunizáció, görbület.

Osztalék, diszkontált pénzáram-módszer, egyszerü osztalék-értékelési modell, Gordon-Shapiro modell, összetett Gordon Shapiro modell, elvárt megtérülés, P/E, EPS.

Ágazati elemzés, üzleti ciklusok, fentröl-lefele ("top-down") elemzés.

Tökepiaci árfolyamok egyensúlyi modellje, CAPM, kockázatmentes hozam, piaci hozam, szisztematikus kockázat, diverzifikálható kockázat, béta, értékpapír-portfólió.

Célkitüzések: Az elsö, részletesen ismertetett modul célja a pénzügy szakos hallgatók számára lefektetni a pénzügyi szemléletmód alapjait, bemutatni az egyes konkrét értékpapírok (részvény és kötvény) értékelésének eltérö módszertanát.

Bevezetésként a hallgatóknak el kell sajátítaniuk bizonyos hasznosságelméleti és kockázattal kapcsolatos fogalmakat, hiszen az értékpapír-befektetések és portfóliók, különösen a részvényportfóliók többfajta kockázattal is rendelkeznek. A hatékony piacok feltevése képezi az értékelés, az egyensúlyi árfolyamok meghatározásának alapját.

Tanácsok a tananyag elsajátításához: Az elméleti fejezet és a szakirodalom tanulmányozása feltétlenül szükséges. Hangsúlyt kell helyezni a feladatok megoldására is, számológép segítségével.

Ezeken túlmenöen ajánlott, hogy a hallgatók egy egységes szemléletet alakítsanak ki az értékpapírértékeléssel kapcsolatosan, amelyben pontosan tudják elhelyezni az egyes diszciplínák (portfólió-menedzsment, pénzügyi elemzés, pénzügyi piacok) szerepét. Ajánlott tehát, hogy ezt a syllabust ezeknek a tantárgyaknak a syllabusával együtt tanulmányozzák.

Kötelezö és ajánlott szakirodalom

Kötelezö szakirodalom: [1] I., III., IV. fejezet

Ajánlott szakirodalom: [2] IV., V. fejezet

KÉRDÉSEK

1. Mit értünk inverz hozamgörbe alatt? Mikor lép fel ez a jelenség? 

2. A kötvény durációjának hármas jelentéstartalma

3. A kötvényárfolyamok konvergencia tulajdonsága

4. Hasonlítsa össze röviden az értékpapírok technikai és fundamentális elemzését           

5. Miért hasznos az értékpapír-portfolió diverzifikációja?

6. A részvények értékelésénél használt P/E-mutató értelmezése, többféle jelentéstartalma.

7. Igaz vagy hamis?

a)     A racionális befektetök általában kockázatsemlegesek

b)     A hasznossági függvény tulajdonképpen biztonságos egyenértékesek sorozata.

c)      Gyengén hatékony tökepiacon a technikai elemzés módszerei nem alkalmazhatók

d)     Ha az értékpapír-piac nem hatékony, az árfolyamok véletlen bolyongást követnek

e)     A racionális befektetök általában kockázatkerülök

f)      Erösen hatékony tökepiacon csak nullához közeli nettó jelenértékü tranzakciók köthetök

g)     A kisebb durációjú kötvény árfolyama kevésbé érzékeny a tökepiaci hozam változására

h)     Ha a piaci hozam kisebb, mint a korrigált kamatláb akkor a kötvény árfolyama felülröl közelít a prémiumos törlesztéshez

i)       A nagyobb görbületü kötvény esetén jobb árfolyam-elörejelzéseket lehet végezni

j)       Az aritmetikai hozamokat elsösorban azért használják, mert idöben összeadhatók (additívak)

k)     A kötvény abban a periódusban kamatimmun, amely a durációjával egyenlö

l)       A logaritmikus hozamokat elsösorban azért használják, mert idöben összeadhatók (additívak)

m)   A törlesztési kockázat kötvények esetén a nemfizetés kockázatát jelenti

n)     Növekedésorientált részvények esetén mindig érdemes alacsony P/E-mutatójú részvényekbe fektetni, hiszen ezek esetében gyors a befektetés megtérülése

I.1.1. Az intertemporális allokáció

Az intertemporális allokációs probléma a jelenlegi fogyasztásról a jövöben remélt többletfogyasztás javára történö lemondás egyéni elemzése és megítélése. Tulajdonképpen minden beruházási és befektetési döntés intertemporális allokációt jelent.

Intertemporális allokáció tökepiac hiányában

Keretfeltételek:

nincs tökepiac, pénz és kamat

egy periódust elemzünk

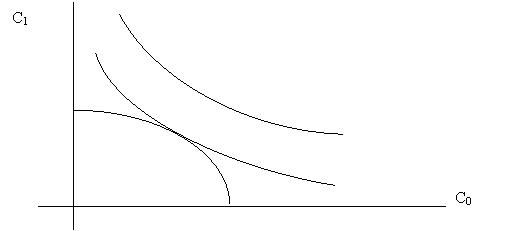
1.     ábra. A jelenlegi és jövöbeni fogyasztás közötti indifferencia (közömbösségi) görbék

Az elemzési keret a fogyasztás beosztása (allokálása) a jelen (C₀) és a jövö (C₁) között.

Az 1. ábrán látható indifferencia görbék tulajdonságai

nem érintik és nem is metszik egymást

pozitívak

konvexek

negatív meredekségüek

A döntéshozó optimumpontja: a szubjektív közömbösségi görbe (konvex) és az objektív fogyasztási lehetöségek görbéjének (konkáv) érintési pontja

A szubjektív idöpreferencia ráta (ip) a semlegességi görbéhez húzott érintö meredeksége az optimumpontban:

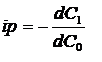
Az intertemporális allokációs probléma megoldása tökepiac hiányában:

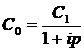
Az idöpreferenciának megfelelöen egységnyi jelenbeni fogyasztás hasznosságát csak nagyobb mennyiségü jövöbeli fogyasztással érhetjük el. Tökepiac hiányában a fenti szubjektív idöpreferencia ráta dönti el, hogy mennyire erösebben preferáljuk a jelenbeni fogyasztást a jövöbelivel szemben?

Intertemporális allokáció tökéletes tökepiacon

A tökéletes tökepiac feltételei:

v    tökéletes információellátás

v    homogén várakozások

2.     súrlódásmentesség: adók és tranzakciós költségek hiánya

v    tökéletes oszthatóság és sokszorozhatóság

v    kompetitív piac: tökéletes verseny

Tökéletes tökepiacon a következö összefüggés érvényesül:

Vagyis az egyéni idöpreferencia ráták aggregálódnak, helyüket átveszi az egységes tökepiaci kamatláb.

v    Fisher szeparáció: tökéletes tökepiacon a személyes idöpreferenciák a tökebefeketetési kritérium szempontjából érdektelenek, a jelenérték növelése az optimális kritérium, annak finanszírozásától függetlenül. Vagyis ilyen piacon a beruházási és finanszírozási döntések szétválaszthatók.

Az intertemporális allokáció megoldása tökéletes tökepiacon:

tehát a szubjektív idöpreferencia helyére az objektív egységes kamatláb lép

I.1.2. A hatékony tökepiacok elmélete

A tökepiaci hatékonyságnak legalább két értelmezését szokás elkülöníteni a szakirodalomban: egyfelöl az ún. információs hatékonyságot, másfelöl a funkcionális hatékonyságot.

Az információs hatékonyság azt jelenti, hogy az árfolyamok mindenkor minden nyilvános információt tükröznek, azaz az új információk árfolyamba való beépülésének sebessége igen gyors, ideális esetben pillanatszerü. Ennek az a következménye, hogy az árfolyamok elörejelezhetetlenek, csakis az összes piaci szereplö számára új információra reagálnak, melynek birtokában nem lehetséges nyereséges kereskedési stratégiákat kiaknázni. Általánosabb értelemben amennyiben mégiscsak sikerülne a piacnál jobb hozamokat rendszeresen elérni, annak biztosan további költségei vannak az információszerzés, a költségesebb elemzök megfizetésének terén, így ezen költségeket is beszámolva, a piac akkor hatékony ha nem sikerül tartós profitokhoz jutni valamilyenfajta bennfentes információ vagy fejlettebb kereskedési stratégia révén.

Ahhoz, hogy az árfolyamok valóban az összes nyilvános és kevésbé nyilvános információt tartalmazhassák, szükség van az úgynevezett funkcionális hatékonyságra is, melynek értelmében a piaci szerkezet, müködés lehetövé kell tegye az olyan sebességü és likviditású kereskedést, amely az arbitrázsügyletek megfelelöen nagy számán keresztül lehetövé teszi, hogy az árfolyamok a belsö érték szintjére álljanak be. Az arbitrázst korlátozó bármilyen technikai akadály (például a rövidre eladás megtiltása) magát a hatékonyságot is korlátozza.

Gyenge hatékonyság: Gyengén hatékony piacokon az árfolyamok minden múltbeli árfolyamalakulásra vonatkozó információt tükröznek.

Közepes hatékonyság: Közepesen hatékony piacokon az árfolyamok minden vállalatra és makrogazdaságra jellemzö releváns nyilvános információt tükröznek.

Erös hatékonyság: Erösen hatékony piacokon az árfolyamok minden vállalati bennfentes információt is tükröznek. Erösen hatékony tökepiacon csak nullához közeli nettó jelenértékü tranzakciók köthetök.

Ebben az értelmezésben a hatékonyság különbözö formái egymásra épülö kategóriák abban az értelemben, hogy az erösebb formák mindig implikálják a gyengébbeket is: az erösen hatékony piac egyben közepesen és gyengén is hatékony, megfordítva azonban nem. Ennek ellenére a gyakorlati tesztelés során pl. a közepes forma tesztelése csupán  eseménytanulmányok segítségével pontatlan, hiszen az új vállalati információk gyors beépülése nem zárja ki azt, hogy korábbi árfolyam-alakulásra alapuló technikai eszközök sikeresek lehetnek. Magyarán a közepes forma pontos tesztelése úgy történhetne, hogy egyszerre végzünk véletlen bolyongás tesztet és eseménytanulmányt is. A gyakorlatban sem a három hatékonysági forma megnyilvánulása sem azok megsérülése nem választható élesen külön.

Hatékony piacokon az árfolyamok véletlen bolyongást követnek ("random walk"). A véletlen bolyongás esetén egy adott napi árfolyam az elözö napi árfolyam és egy véletlen változó összege:

Technikai elemzés: Az árfolyamokat mozgató tökepiaci információk rövid távú alakulását vizsgálja egyedi matematikai statisztikai eszközök, illetve grafikonok segítségével. Egy legalább gyengén hatékony tökepiacon a technikai elemzés értelmetlen, nem vezet gazdaságilag szignifikáns profitokhoz.

Fundamentális elemzés: Az ún. belsö vagy fundamentális értéket kívánja megbecsülni a reálgazdasági folyamatok és a vállalati szintü pénzügyi mutatók segítségével. Egy legalább közepesen hatékony tökepiacon a fundamentális elemzés értelmetlen, nem vezet gazdaságilag szignifikáns profitokhoz.

Passzív portfóliómenedzsment: Az erösen hatékony piacokon nem lehetséges szisztematikusan jobban teljesíteni a piaci portfóliónál ezért a jövedelmezö stratégia a piaci indexbe való befektetés (passzív stratégia).

Aktív portfóliómenedzsment: Ha a tökepiac nem hatékony keresni lehet alulárazott értékpapírokat ("stock selection") vagy idözíteni lehet, hogy mikor érdemes kötvénybefektetéseket részvénypiaci befektetésre cserélni és fordítva (piaci idözítés, "market timing"). Erösen hatékony piacokon az aktív stratégia értelmetlen, nem vezet szignifikáns profitokhoz.

I.1.3. Hasznosság és kockázat:

A befektetö befektetési döntésének keretrendszere a mikroökonómiából ismert hasznosság-elemzés valamint a befektetö kockázattal szembeni magatartása (kockázati attitüdje). Hagyományosan a befektetök a várható érték-variancia szabályt alkalmazzák.

Várható érték - variancia () szabály:

Azt a befektetést preferáljuk, amely azonos kockázati szinten nagyobb várható értéket kínál vagy azonos várható értékhez kisebb kockázatot rendel.

Hasznossági függvény: A vagyon egyes értékeihez (w) szubjektív értéket rendel: U(w)

Kockázati magatartás (attitüd):

A kockázattal szembeni szubjektív viszony, a kockázat-megtérülés átváltás egyéni értelmezése. A kockázati attitüd szempontjából beszélhetünk kockázatkerülö, kockázatsemleges és kockázatkeresö befektetökröl.

Kockázatkerülö magatartás:

A kockázatkerülö döntéshozó hasznossági függvénye konkáv és növekvö (a csökkenö határhaszon törvényének megfelelöen). A racionális befektetök kockázatkerülök.

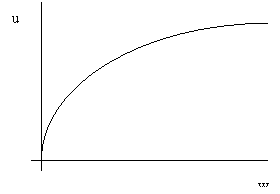
3.     Ábra. Kockázatkerülö befektetö hasznossági függvénye

Kockázatkeresö magatartás:

A kockázatkerülö döntéshozó hasznossági függvénye konvex és növekvö (nem érvényesül a csökkenö határhaszon törvénye). A közgazdaságtan a kockázatkeresést irracionális magatartásnak tekinti.

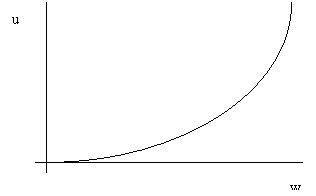
4.     Ábra. Kockázatkeresö befektetö hasznossági függvénye

Kockázatsemleges magatartás:

A kockázatsemleges befektetö számára minden vagyon-növekmény ugyanakkorra hasznosságtöbbletet eredményez, a befektetö érzéketlen a kockázatra.

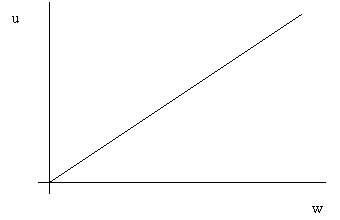
5.     Ábra. Kockázatsemleges befektetö hasznossági függvénye

Biztonságos (kockázatmentes) egyenértékes ("Certainty equivalent", CEQ): Az a biztos vagyonösszeg, amely ugyanazzal a hasznossággal rendelkezik, mint a vizsgált kockázatos vagyonösszeg:

6.     Ábra. Kockázatkerülö befektetö biztonságos egyenértékese (CEQ) és kockázati prémiuma (RP)

W1 és W2 -  az összvagyon két tetszöleges szintje

E(w) - a vagyon várható értéke (kockázatos összeg!)

CEQ(E(w)) - az E(w) kockázatos összegnek megfelelö biztonságos egyenértékes (biztos összeg!)

A 6.ábra értelmezése az, hogy racionális befektetö esetén a kisebb, de biztos pénzösszeg ugyanannyi hasznossággal rendelkezik mint egy nagyobb, de bizonytalan (kockázatos) összeg.

A kockázatkerülés erösségét méri az Arrow - Pratt féle abszolút kockázati tartózkodás mutató:

Kockázati prémium ("Risk premium", RP):

A kockázati prémium az egyén hasznossági függvényétöl, pontosabban annak deriváltjaitól függ, ugyanakkor a kockázati prémium egyenlö a kockázatos összeg várható értéke és a neki megfelelö biztonságos egyenértékes közötti különbséggel.

Kockázatkerülö befektetö esetén: RP>0 (csak többletmegtérülés fejében vállal kockázatot)

Kockázatsemleges befektetö esetén: RP=0

Kockázatkeresö befektetö esetén: RP>0 (még ö fizet azért hogy a kockázatos játékban, befektetésben részt vehessen)

Kilátáselmélet ("prospect theory")

A kilátáselmélet egy alternatív megközelítés a klasszikus hasznosságelméleti modellhez képest, amelyben az egyéni, befektetöi pszichológia torzításai is megjelennek. A kilátáselméletben egy döntési alternatíva értékét nem a kimenetek hasznossága határozza meg, hanem az hogy a kimenetek mennyivel járulnak hozzá a vagyoni helyzet megváltozásához?

Feltételezések:

a csökkent arányosság elve: az észleléshez képest a reakciók tompítottabbak, a szubjektum eltorzítja a valóságot

aszimmetria: egy adott állapothoz képesti elmozdulásra nem szimmetrikusak a döntéshozó reakciói: a vagyoni helyzet csökkenésére érzékenyebben reagálunk, mint annak növekedésére.

A vagyoni változására történö reagálás nagyrészt a vonatkoztatási ponttól (jelenlegi vagyoni helyzettöl) függ.

A kilátáselmélet hipotetikus értékfüggvénye:

7.     A befektetö értékfüggvénye a kilátáselméletben

Az értékfüggvény tulajdonságai:

a nyereség szakaszán konkáv ekkor a befektetök általában kockázatkerülök

a veszteséges szakaszon konvex, a befektetök kockázatbaráttá válnak

nem szimmetrikus: a veszteséges szakasz meredekebb mint a nyereséges, a konvexitás nagyobb mértékü mint a konkavitás: azaz a veszteség okozta bánat erösebb mint a nyereség okozta öröm

A bekövetkezési valószínüségek észlelése a döntési súlyfüggvény segítségével történik.

A súlyfüggvény azt mutatja, hogy a szubjektív preferenciák és a torzult észlelés mennyire érzékenyes követi a valószínüségeloszlást.

A kilátáselmélet hipotetikus döntési súlyfüggvénye:

8.     A befektetö döntési súlyfüggvénye a kilátáselméletben

A súlyfüggvény tulajdonságai:

csökkent arányosság elve: a döntéshozatalban a legvalószínübb eseményeket a döntéshozók alulbecsülik, az extrém eseményeknek pedig a normálisnál nagyobb valószínüséget tulajdonítanak.

A kilátáselmélet abszolút kritériuma: Akkor érdemes a befektetési alternatívát megvalósítani, ha a döntési súlyokkal képzett értékfüggvénye pozitív:

I.2. KÖTVÉNYEK ÉRTÉKELÉSE

A kötvény általában fix kamatozású hosszú lejáratú hitelviszonyt megtestesítö átruházható értékpapír. A kötvény tulajdonosa a kamatok és a névérték törlesztésének bizonyos sorozatára jogosult.

Névérték: A tartozás névleges összege, a kibocsátó általában ezen az árfolyamon vásárolja vissza a kötvényt annak birtokosától. Olykor ennél nagyobb árfolyamon vásárolják vissza a kötvényt, ilyenkor a kötvény törlesztési prémiummal (T) rendelkezik.

Névleges kamatláb (szelvénykamatláb): Az éves kamat a névérték százalékában.

Árfolyam: Adott névértékü kötvény pillanatnyi piaci ára általában a névérték százalékában kifejezve.

A kötvényárfolyam paritásos, ha megegyezik a kötvény által biztosított pénzáramlások jelenértékével.

Pari alatt jegyzett (alulértékelt) a kötvény, ha árfolyama kisebb, mint pénzáramainak jelenértéke, ellenkezö esetben pari felett jegyzett (felülértékelt).

A kötvények föbb típusai:

Elemi kötvény (zérokupon kötvény): nem fizet szelvénykamatot, hanem egyetlen jövöbeli idöpontban (a lejáratkor) teljesít kifizetést. Kibocsátása diszkontárfolyamon történik. A kötvénybefektetö nyeresége a névérték és a kibocsátási diszkont árfolyam különbsége.

Kamatszelvényes (klasszikus) kötvény: rendszeres idöközönként szelvénykamatot fizet, általában névértéken bocsátják ki, a névértéket pedig a lejáratkor egy összegben törlesztik vagy a futamidö alatt egyenletesen ("sinking fund").

Opciós tulajdonságú kötvények:

1.Visszahívható kötvény: egy elöre meghatározott idö után a kibocsátó egy elöre rögzített árfolyamon visszavásárolhatja a kötvényét.

2.Átváltható kötvény: a kötvénybefektetö meghatározott számú részvényre válthatja át kötvényét, amely az átváltásig kötvényként az átváltás után részvényként viselkedik

3.Opciós utalványos (warrantos) kötvény: általában egy hosszú lejáratú opció, amelyet egy vállalat saját részvényeire vagy kötvényeire bocsát ki. Az átválthatóval szemben az utalvány egy különálló értékpapírként funkcionál, érvényesítéskor készpénzben ki kell fizetni a szóban forgó opcióban megnevezett részvények árát.

Államkötvény: Az államkincstár (pénzügyminisztérium) által kibocsátott, egy évnél rövidebb kincstárjegy vagy egy évnél hosszabb lejáratú szelvényes kötvény.

Önkormányzati kötvény: a helyi közigazgatási egységek által kibocsátott rendszerint adómentes kötvények

Vállalati kötvény: Magán vagy állami vállalatok által kibocsátott kötvények, eltérö kockázati szintjük miatt eltérö hozamígérettel rendelkeznek, figyelni kell a kötvényminösítö vállalatok minösítéseire.

Euro (xeno) kötvény: egy, a kibocsátás helyéhez képest külföldi devizában jegyzett államkötvény-kibocsátás. Pl. USD- denominált kötvények kibocsátása Japánban.

Kötvények jelenérték-orientált értékelése:

Hatékony kötvénypiacon a kötvény egyensúlyi árfolyama a kötvény jövöbeli pénzáramlásainak jelenértékével egyenlö.

Felhasznált jelölések:

P - a kötvény árfolyama

r- piaci hozam (kalkulatív kamatláb)

N- névérték

k- névleges (szelvény-) kamatláb

T- végsö törlesztés (ami prémium esetén nagyobb a névértéknél)

n- futamidö

A kötvények egyensúlyi árfolyamára a következö összefüggések érvényesek (levezetésükhöz lásd a Pénzügymatematikai kurzust- syllabust):

Kamatszelvényes kötvény:

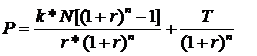
ugyanez abban az esetben ha a kötvény egy éven belül többször is  kamatozik:

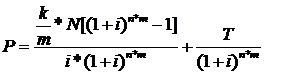
vagy

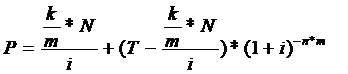
ahol

 a kamatperiódusra jutó kamatláb

m-éven belüli szelvényfizetések száma

Zérokupon kötvény: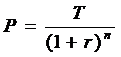

Annuitásos kötvény:

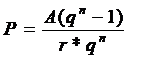
ahol A az annuitás, azaz a kamat és a névérték törlesztörészletének éves szinten azonos összege.

Örökjáradék (konzol) kötvény:

A fent ismertetett árfolyamok úgynevezett nettó árfolyamok ("clean price"), nem tartalmazzák az idöarányos kamatot ("accrued interest"). Ezzel szemben a bruttó árfolyamok az idöarányos kamatot is tartalmazzák:

Bruttó árfolyam = nettó árfolyam + k*N* n₁/n₂

ahol

n₁ - az utolsó szelvényfizetés óta eltelt napok száma

n₂ - a napok száma egy évben (az egyes konvenciók függvényében eltérö lehet pl. 365 vagy 360)

korrigált kamatláb: 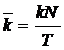 (ezt abban az esetben számoljuk, ha nem névértéken, hanem prémiummal történik a végsö törlesztés, T≠ N.

A kötvényárfolyamok konvergencia tulajdonsága:

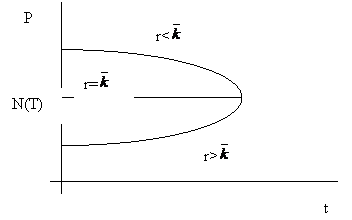
9.     ábra. A kötvényárfolyamok konvergencia tulajdonsága

A kötvényárfolyam a lejárathoz közeledve a névértékhez tart. Természetesen, ha prémiummal történik a törlesztés, akkor az árfolyam a prémiumot is tartalmazó végsö törlesztörészlethez (T) tart. A 9. ábra a nettó árfolyamok konvergenciáját szemlélteti.

1. Ha a piaci hozam nagyobb, mint a kötvény korrigált kamatlába (r>) akkor a kötvényárfolyam alulról közelíti a névértéket (vagy végsö törlesztést).

2. Ha a piaci hozam kisebb, mint a kötvény korrigált kamatlába (r<) akkor a kötvényárfolyam felülröl közelíti a névértéket (vagy végsö törlesztést).

A kötvények hozam-orientált értékelése

A kötvény belsö megtérülési rátája (lejárati hozama)

Az a hozamráta, amely mellett a kötvény pénzáramainak jelenértéke éppen megegyezik a piaci árfolyammal, tulajdonképpen a kötvény belsö megtérülési rátája.

Az egyes kötvényfajták esetén a következö képletek érvényesek a lejárati hozamra:

A zérókupon kötvény effektív lejárati hozama: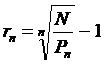

Tulajdonképpen egy belsö kamatlábnak felel meg a kamatos kamat szabályai szerint

A zérókupon kötvény folytonos hozama (loghozama)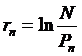

A logaritmikus hozamokat (loghozamokat) elsösorban additív tulajdonságuk miatt használjuk (pl. a heti loghozam a napi loghozamok összege).

Kamatszelvényes kötvény esetén többfajta hozam is használatos:

Szelvényhozam ("current yield", CY):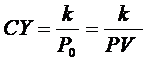

Tulajdonképpen a kötvény szelvénykamatát mutatja a kötvényárfolyam százalékában.

Egyszerü lejárati hozam ("simple yield to maturity", SYTM)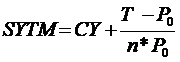

A szelvényhozamhoz még hozzáadjuk annak az árfolyam-nyereségnek a hozamát, amit a kötvény lejáratig tartásából kapunk.

A kamatszelvényes kötvény teljes lejárati hozama általában sajnos csak megközelítöleg számolható ki a következöképpen:

Teljes lejárati hozam ("Yield to maturity", YTM) közelítö számításának módja:

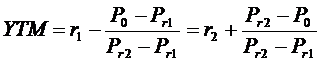
ahol r₁ és r₂ próbakamatlábak (mi magunk határozzuk meg találgatásos alapon), P₀, P_r1 és P_r2 pedig a kötvény jelenlegi árfolyama illetve az árfolyam, amennyiben a hozam r₁ illetve r₂ lenne (r₁ illetve r₂ behelyettesítése az árfolyamképletbe).

Mivel a SYTM jó közelítése a YTM-nek ezért elsö próba-hozamrátának az SYTM-et választhatjuk:

r₁ = SYTM  r₂ pedig 1%-al tér el r₁ - töl.

Ez egy lineáris interpoláció két próbakamatlábat (r₁ és r₂) felhasználva:

Ha a P(r₁)<P₀ akkor r₂> r₁- et kell választani ellenkezö esetben r₂ < r₁

Ex post hozam, annak átlaga, szórása:

Ha a kötvénybefektetés átfogó megtérülésére vagyunk kíváncsiak, akkor azt is figyelembe kell venni, hogy a kötvényszelvények beváltásából származó készpénz legalábbis a mindenkori tökepiaci kamatláb mellett kamatoztatható a kötvény lejáratáig. Erre szolgál a kötvény ex post hozama:

 

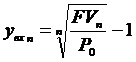
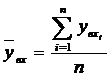
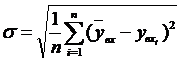
Az ex post hozam számításához elsösorban a kötvény szelvénykamatainak újrabefektetéséböl származó jövöértéket (FV_n) kell meghatározni a kamatos kamat szabályai szerint.

Reál hozam: az infláció hatásától megtisztított hozam:

                       

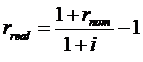
ahol i az inflációs rátát jelöli

Hozamgörbe (a kamatlábak lejárati szerkezete):

Az azonos típusú és kockázatú kötvények hozamait ábrázolja a lejárat (idö) függvényében

Típusai:

1.     Normál hozamgörbe (emelkedö):

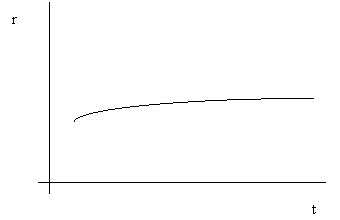
A normál hozamgörbe magyarázata:

Hosszabb lejáratokhoz magasabb hozamok tartoznak, mert:

a befektetök többlethozamot várnak el, amiért likviditásról mondanak le (likviditáspreferencia-elmélet)

hosszabb távon enyhe inflációs várakozások tapasztalhatóak (várakozási elmélet)

2. Inverz hozamgörbe:

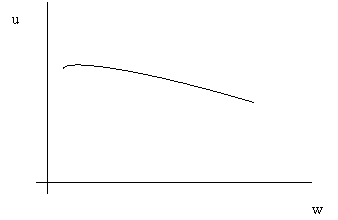
erös dezinflációs várakozások esetén tapasztalható

2.     Púpos hozamgörbe:

A Kötvények Kockázati Elemzése

Kamatkockázat

A kamatlábak (piaci hozamok) és a kötvény árfolyama ellentétes irányban mozognak, a hozam emelkedése csökkenti a kötvény árfolyamát. A kötvény árfolyama tehát változik (kockázatos) a kamatláb (hozam) változásának függvényében.

Minden egyes kötvény eltéröen reagál a piaci hozam megváltozására. A hozamváltozás árfolyamra gyakorolt hatása több tényezötöl is függ:

a kötvény pénzáramainak idöbeli struktúrája

a hozamváltozás erössége és iránya

a kötvény lejárata

A kötvény durációja (átlagideje)

A kötvény kamatkockázatának mérésénél fontos eszköz a kötvény durációja (átlagideje).

A duráció az egyes kifizetésekig hátralevö idötartamok súlyozott számtani átlaga, ahol a súlyokat az egyes kamatfizetések jelenértéke és a kötvény teljes jelenértékének (árfolyamának) aránya határozza meg:

            

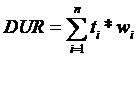
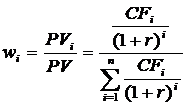
A duráció és az árfolyamváltozás kapcsolata az úgynevezett volatilitáson vagy módosított duráción keresztül valósul meg:

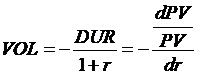
A duráció hármas jelentéstartalma:

1. Az értelmezés alapján a duráció egyfajta dinamikus megtérülési idö ezért az alacsonyabb durációjú kötvény preferálható
2. A fenti összefüggés azt mutatja, hogy a hozamváltozásra az árfolyam a módosított duráción keresztül hat, vagyis a duráció a kötvény hozamérzékenységét méri. Ilyen értelemben is a kisebb durációjú kötvény preferálható, hiszen a kisebb durációjú kötvény kevésbé kitett a hozamváltozási kockázatnak.
3. A duráció az az idöpont, amelyben a kamatlábváltozás árfolyamra gyakorolt hatását (pl. csökkenését) éppen kiegyenlíti a kamatszelvények ujrabefekektetéséböl származó végértékre gyakorolt hatás. Ezért a duráció idöpontját immunácis idöszaknak is nevezzük. Teljes kamat-immunizációt akkor hajthatunk végre, ha zéró átlagidejü kötvényportfólióba fektetünk be.

Zérókupon kötvény durációja: DUR = n

Kamatszelvényes kötvény durációja

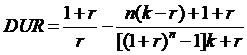
Annuitásos kötvény durációja: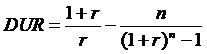

Örökjáradék-kötvény durációja: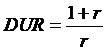

Görbület (konvexitás)

A duráción kívül az ún. "görbület"-nek is szerepe van a kamatkockázat értékelésében.

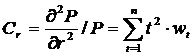
A görbület a kötvényárfolyam hozam szerinti második deriváltjának és az árfolyamnak a hányadosa:

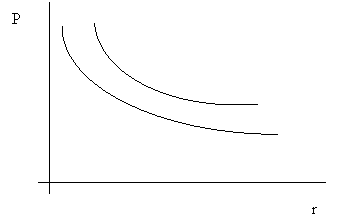
10.  Ábra. Kötvények eltérö görbülettel

A fenti ábrán a felsöbb kötvény nagyobb görbületü, ami elönyösebb a kötvénybefektetönek, hiszen hozamemelkedés esetén kisebb árfolyamveszteséget könyvelhet el, hozamcsökkenés esetén pedig nagyobb árfolyamemelkedésre számíthat.

Árfolyam-változás elörejelzés logkamatlábbal (folytonos kamatlábbal)

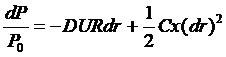
Ez a képlet azt mutatja, hogy úgy kaphatunk pontosabb elörejelzést a kötvényárfolyam-megváltozására, ha a duráción kívül a görbület hatását is figyelembe vesszük.

II.2. Részvények értékelése

A részvény a vállalati nyereségre és vállalati szavazati jogokra feljogosító forgatható értékpapír. A kötvénynél kockázatosabb, hiszen nem fix jövedelmezöségü, és lejárata sincs pontosan meghatározva.

Makrogazdasági és ágazati elemzés

A makrogazdasági és ágazati elemzéskor azokat a vállalaton kívüli tényezöket elemezzük, amelyek egy adott részvény hozamára, szisztematikus kockázatára befolyást gyakorolnak. A következökben az egyes makroökonómiai változókat nem csupán abszolút értékük vagy növekedési ütemük szempontjából kell tekinteni, hanem a rájuk vonatkozó elörejelzések szempontjából is, hiszen ezen elörejelzések szolgáltatják az alapot a jövöbeli osztalékáramok megbecsülésére, ami pedig a részvényárfolyam meghatározó tényezöje.

A részvények felülröl-lefele ("top-down") történö elemzése a következö lépéseket foglalja magába:

1.     Világgazdaság elemzése. A világgazdaság és a meghatározó fejlett tökepiacok mozgásai még a legtávolabbi tözsdék egyedi értékpapírjaira is kifejtik hatásukat. A feltörekvö és a fejlett tökepiacok között igen gyakran együttmozgás, kointegráció tapasztalható vagy pedig a fejlett piacokról nagyon hamar átterjednek a hatások a feltörekvö piacokra (átcsordulás, "spillover"). A világgazdaság elemzése különösen jelentös, ha külföldi értékpapír-befektetéseink vannak, ekkor a mérvadó devizaárfolyamot is figyelemmel kell kísérni.

2.     A belsö gazdaság elemzése. A belsö gazdaság tekintetében igen fontos figyelemmel kísérni a következö mutatókat: a bruttó hazai termék (GDP), annak egy före esö nagysága, az inflációs ráták és elörejelzések, kamatlábak, a költségvetés és a folyó fizetési mérleg egyenlege (szufficit vagy deficit). Ezeken túlmenöen fontos a gazdaság (termelök és fogyasztók) általános hangulata, a befektetök tözsdei bizalmi szintje, amelyre az utóbbi évtizedekben egyre jobban odafigyelnek ám még mindig meglehetösen nehéz ezeket a változókat mérni.

3.     A monetáris politika elemzése. A fejlett tökepiacok befektetöi és kereskedöi nagy kíváncsisággal követik az amerikai Szövetségi Tartalék (Fed) kormányzójának bejelentéseit, elörejelzéseit. Hasonlóan Romániában is nagy figyelemmel követik a Nemzeti Bank kormányzójának bejelentéseit. Ennek két oka van:

-egyfelöl a Jegybank elörejelzései is intézkedései információt szolgáltatnak a gazdaság egész sor mutatójának helyzetéröl (ezeknek a bejelentéseknek gazdaság-diagnosztikai értékük van)

- másfelöl az irányadó kamatláb megváltoztatása azonnal kihat a tözsdei részvények és kötvények árfolyamára is.

4.     A fiskális (költségvetési) politika elemzése. A költségvetési politika is meghatározó, hiszen az általános közkiadások szintje, a kormányzat belsö és külsö eladósodottságának mértéke elsösorban ezen deficitek kiegyensúlyozására kibocsátott állampapírok hozamára gyakorol hatást. Ugyanakkor egyes fiskális politikák, pl. kínálat oldali ösztönzök, adócsökkentések kedvezöen hathatnak a részvények árfolyamára, de csak akkor, ha egyébként a belsö gazdaság állapota ezt lehetövé, fenntarthatóvá teszi.

5.     A gazdasági és üzleti ciklusok elemzése. Az egyes gazdasági ágazatok lehetnek többé vagy kevésbé érzékenyek az általános üzleti ciklus mozgásaira.

Az olyan befektetök, akik "ciklikus" ágazatokba fektetnek (pl. építöipar, gépkocsi-ipar) fokozottan figyelik az üzleti ciklus alakulását.

6.     Ágazati elemzés. Az ágazati elemzéskor az elsö nehézség egy befektetö útjában éppen az egyes ágazatok pontos körülhatárolása, szétválasztása. Egy következö szempont annak a meghatározása, hogy az illetö ágazat mennyire érzékeny a gazdasági-üzleti ciklusokra? Az "ágazati váltás" mint befektetési stratégia ("sector rotation") azt feltételezi, hogy az üzleti ciklus szakaszának függvényében döntjük el, hogy milyen ágazatba fektetünk be? Természetesen az ágazati váltás is aktív befektetési stratégia, és mint ilyen, nem sok haszonnal kecsegtet egy teljesen hatékony tökepiacon. Ezeken túlmenöen az értékpapírelemzök további ágazat-specifikumokra is kitérnek, mint pl. a piac szerkezete ("SCP modell") vagy az ágazat szerkezete a Porter-féle öt "erö" függvényében.

Pénzügyi elemzés: a felülröl lefele megközelítés következö lépcsöje a részvényt kibocsátó vállalat általános pénzügyi elemzése, diagnosztizálása. Ebben a szakaszban a következö pénzügyi mutatók elemzésére van szükség:

1.     Szintetikus kimutatások:

Számviteli mérleg

Eredménykimutatás

Pénzáram-kimutatás

2.     Megtérülési mutatók:

Sajáttöke-arányos megtérülés ("Return on equity", ROE)

Eszközarányos megtérülés ("Return on asserts", ROA)

Tökeáttételi mutató: Kölcsöntöke / saját töke

ROE felbontása (DuPont séma)

3.     Forgótöke-gazdálkodási mutatók

Készletek forgási sebessége

Forgótöke forgási sebessége

Követelések átlagos behajtási ideje

stb

4.     Likviditási mutatók

általános likviditás

likviditási gyorsráta

kamatfizetési mutató

stb

5.     Piaci mutatók

Piaci érték - könyv szerinti érték hányados (P/B, "Price-to book value")

Osztalékhozam (DY, "dividend yield"): a legutóbb kifizetett osztalék és az árfolyam hányadosa

P/E mutató ("Price - earnings ratio", árfolyam-nyereség hányados)

PEG mutató ("Price - earnings to growth ratio"), a P/E mutató korrekciója, amely megtisztítja a P/E mutatót az elvárt növekedés hatásától

Stb.

Részvények fundamentális, jelenérték-alapú értékelése

Jelölések:

D, DIV - osztalék

P - részvényárfolyam

Re -részvényektöl elvárt megtérülés (részvénytöke költsége)

g - osztalékok (vagy a nyereség) növekedési üteme

Hatékony piacokon a részvény egyensúlyi árfolyama a jövöbeli várható osztalékáramok jelenértéke:

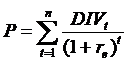
Ami a következökre egyszerüsödik az egyes értékelési modellek esetén:

Konstans osztalék esetén (örökjáradék)

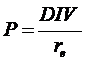
Gordon - Shapiro (konstans osztalék-növekedési modell)

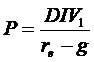
A Gordon-Shapiro értékelési modellt csak akkor használhatjuk, ha az elvárt hozam (r_e) nagyobb, mint az osztalék növekedési üteme (g)

Az osztalékok növekedési üteme meghatározható pl. a következöképpen:

g = ROE * b

ahol ROE (Return on equity) - a részvényegységre jutó megtérülés

b = az újrabefektetési ráta = 1- osztalékkifizetési ráta

Részvényegységre jutó nyereség (Earnings per share, EPS):

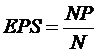
ahol NP - nettó profit

N - forgalomban levö részvények száma

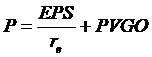
Ez a képlet azt mutatja, hogy a részvényárfolyam egyik részét az EPS-en keresztül a vállalati eredmények (nyereség) befolyásolja, másik összetevöje pedig az úgynevezett növekedési lehetöségek jelenértéke (PVGO). Ha az elsö összetevö nagyobb, akkor érték-részvényröl ("value stock") beszélünk, ha pedig a második, akkor "növekedési" részvényröl ("growth stock").

Árfolyam-nyereség (P/E, PER) hányados:

A P/E mutató azt mutatja, hogy egységnyi vállalati nettó nyereséget mennyire értékel (áraz be) a piac?

A P/E mutató értelmezéséhez azt mindig a hasonló gazdasági ágazatban müködö és azonos kockázati szinttel jellemezhetö vállalatok P/E értékével kell összehasonlítani.

A relatíve alacsony P/E érték a fundamentális elemzök szerint alulértékelt részvényre utal.

A P/E mutatót olyan vállalkozások részvényei esetén érdemes a leginkább alkalmazni, amelyeknél nincs elörejelzett növekedés az osztalékokat illetöen.

A P/E mutató másik értelmezése szerint az tulajdonképpen egy megtérülési idö jellegü mutató tehát az alacsony P/E értékü részvényekbe befektetett

Amennyiben nem feltételezünk növekedést, tehát a nettó nyereséget teljes egészben osztalékok formájában fizetik ki (nincs visszaforgatott profit) akkor a részvényektöl elvárt hozam a P/E mutató alapján is meghatározható: 

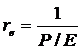
növekvö osztalékáram esetén:

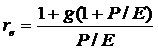
A P/E mutató hiányosságai

Az elsö számú hiányosság, hogy a nevezöben szereplö mennyiség a számviteli alapon számolt és bejelentett részvényegységre jutó nyereség. Különösen az elmúlt évtized nagyvállalati botrányai (Enron, Worldcom, stb) irányították ismét a figyelmet arra, hogy a számviteli mutatók nem mindig megbízhatóak.

Egy másik zavaró tényezö az, hogy az elmélet által használt P/E mutató a következö idöszak elörejelzett nyereségeit használja fel (E₁), míg a gyakorlatban, különösen a pénzügyi szaksajtóban közzétett P/E mutatók a legutóbb közzétett nyereséget (E₀) vetítik részvényegységre.

Harmadszor, a P/E mutató értékei igencsak változékonyak a gazdasági ágazat függvényében. Általában a fiatal, információs, kommunikációs vagy éppen biotechnológiai szektorokban tapasztalhatunk nagyobb P/E mutatókat, míg a nagy múltra visszatekintö energetikai vagy kitermelö "fejöstehenek" alacsonyabb P/E értékekkel rendelkeznek.

Ugyancsak jellemzöen magasabb P/E mutatók tapasztalhatóak a feltörekvö piacokon ahol a jövöbeli potenciális növekedés az, ami a magas P/E mutatót eredményezi.

Részvény-hozamok:

Tényleges (ex post) hozamok:

1. Aritmetikai hozamok:

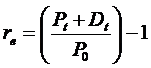
ahol P_t illetve a P₀ az árfolyam a végsö illetve kezdö idöpontban D_t pedig a t idöszakban esedékes osztalék

2. Loghozam:

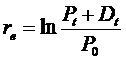
Az elvárt hozam a tökepiaci árfolyamok egyensúlyi modellje ("Capital Asset Pricing Modell", CAPM) alapján:

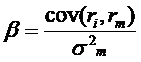
a szisztematikus kockázat méröszáma. Abból származik, hogy az értékpapírpiaci termékek hozama között együttmozgás (korreláció) tapasztalható, ezért a szisztematikus kockázat nem szüntethetö meg diverzifikáció segítségével (nem diverzifikálható kockázat). R_m a piaci portfólió (tözsdeindex) hozama, r_f pedig a kockázatmentes (kötvény) hozam.

A CAPM modell egyszerü értelmezése: Minél nagyobb a szisztematikus kockázat (béta), annál nagyobb megtérülést vár el a piac az illetö értékpapírtól.

MEGOLDOTT FELADATOK

1. Egy 100 Ft névértékü kötvény hátralevö futamideje 4 év, kamatszelvénye 18%. A törlesztés az utolsó 3 évben esedékes, 50-25-25%-os részletekben. A hasonló kamatozású és futamidejü kötvényektöl elvárt hozam 25%.

a)     Írja fel a kötvény pénzáramlását

b)     Mennyit fizetne most ezért a kötvényért?

Megoldás a)

b)

2. Egy kötvény névleges kamatlába 8%, árfolyama 80. A lejáratig hátralevö idö 5 év. A lejáratig 20 Ft árfolyamnyereségre teszünk szert. Mekkora a kötvény szelvényhozama és egyszerü lejárati hozama?

Megoldás

      

3. Adottak a következö zérókupon kötvény árfolyamok: P1=0,9 P2=0,8 P3=0,7.

Határozzuk meg az azonnali hozamok görbéjét

Megoldás

   

4. Mennyi 10% piaci kamatláb mellett az évi 80 RON örökjáradék-kötvény árfolyama, átlagos hátralevö futamideje (durációja) és volatilitása? Hány százalékkal változik az árfolyam ha a piaci kamatláb 10,1%-ra nö?

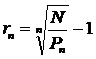
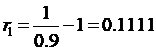
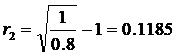
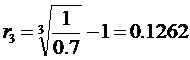
Megoldás

a) P=80/0,1=800 RON

DUR=(1+r)/r=1,1/0,1=11 év

VOL=-DUR/(1+r)=-11/1,1=-10 év

b) dP/P = VOL * dr = - 10*0,1%= -1%

5. Adott egy 5 éves futamidejü, 18% névleges kamatozású kamatszelvényes kötvény. A piaci hozam 20%. Mennyi idö múlva lesz a kötvény végértéke immunis a piaci hozam változásaira?

Megoldás

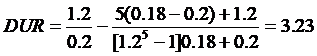  év

Az A kötvény névleges kamatlába 10%, a B kötvényé 20% (3 év lejáratúak) és ismertek a következö elemi kötvényárfolyamok: P1=0,9, P2=0,8, P3=0,7. Melyik kötvényt vásárolná meg, ha bizonytalan irányú de jelentös kamatláb-változásra számít?

Megoldás

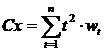
A 3-as feladatban kiszámolt piaci hozamokat kell felhasználni az egyes idöszakokhoz tartozó súlyok (w) kiszámításához:

Azt amelyiknek nagyobb a görbülete:

Hasonlóan Cx(B)=7,101 ezért az "A" kötvényt választjuk

6. A Saláta Rt. jövö évi osztaléka várhatóan 120 RON, az elemzök szerint évi 10%-os növekedési ütem várható töle. A részvénytöl elvárt hozam 20%. Mekkora a részvény reális (fundamentális) árfolyama?

Megoldás

7. Az XY Rt. jövö évi osztaléka várhatóan 120 Ft, az elemzök szerint évi 10%-os növekedési ütem várható töle. A részvénytöl elvárt hozam 8%. Mekkora a részvény reális (fundamentális) árfolyama?

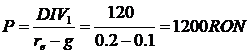
Megoldás

Mivel g>r ezért nem határozható meg az egyensúlyi árfolyam

8. A Tengely Rt. várhatóan három éven keresztül évi 100 Ft osztalékot ad, majd ez évi 10%-os ütemben fog növekedni. A cégtöl elvárt hozam évi 25%. Mekkora a részvény reális árfolyama?

Megoldás

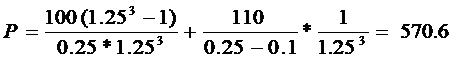
4. Mekkora a részvény osztalékainak növekedési üteme, ha az árfolyama 120 Ft, a jövö évi osztalék 10 Ft, a kockázatmentes kamatláb 10%, a piaci hozam 15% és a részvény bétája 0,8?

Megoldás

R_e=10%+1,8*8%=24,2%

g = r_e- DIV₁ / P = 0,244 - 10 / 125 = 16,4%

8. Mekkorára becsüli a piac a részvény növekedési lehetöségeinek jelenértékét, ha az árfolyama 120 Ft, a jövö évi részvényegységre jutó nettó nyereség 10 Ft, a kockázatmentes kamatláb 10%, a piaci hozam 15% és a részvény bétája 0,8?

Megoldás

  

9. Egy részvény jövö évi osztaléka 60 RON. Ez az érték az elörejelzések szerint évi 12%-al fog növekedni. Az elvárható éves hozam (kalkulatív kamatláb) 15%. Mekkora az elméleti árfolyam?                    

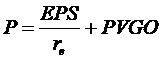
Megoldás

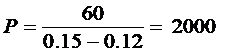
3. Egy részvény idei osztalékát, 60 RON-t holnap fogják kifizetni a részvény tulajdonosának. Ez az érték az elörejelzések szerint évi 12%-al fog növekedni. Az elvárható éves hozam (kalkulatív kamatláb) 15%. Mekkora az elméleti árfolyam?         

Megoldás

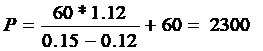
II. MODUL. PORTFÓLIÓ-ÉRTÉKELÉS

Alapfogalmak: szisztematikus kockázat, diverzifikálható kockázat, béta, értékpapír-portfólió, Markowitz-féle hatékony határvonal, optimális portfólió, portfólió-hozam, portfólió variancia, a teljes kockázat felbontása.

Tökepiaci árfolyamok egyensúlyi modellje, CAPM, kockázatmentes hozam, piaci hozam, értékpapírpiaci egyenes (SML), tökepiaci egyenes (CML), karakterisztikus egyenes (SCL), arbitrázs-értékelési modell (APT), többtényezös (multifaktor) modellek.

Portfólió-konstrukció, peer-group, benchmark, Bottom-up, top-down portfólió-konstrukció.

Aktív portfoliómenedzsment, passzív portfoliómenedzsment, Sharpe, Treynor, Jensen mutatók, Treynor-Black modell.

Célkitüzések: A második modulban azt vizsgáljuk, hogy milyen értékelési módszerek állnak rendelkezésre az értékpapírok kombinációjából származó portfóliók értékelésére?

A legfontosabb gondolat a szisztematikus és nem szisztematikus kockázat szétválasztása, a hozam-kockázat átváltási viszony elsajátítása. Ezekre épülnek a legnépszerübb egyensúlyi árfolyammodellek: a CAPM és az APT.

Tanácsok a tananyag elsajátításához: Az elméleti fejezet és a szakirodalom tanulmányozása feltétlenül szükséges.

Értékpapír-értékelés és portfólió-értékelés tekintetében igencsak böségesen állnak rendelkezésre Internetes források is, ezek különösen rávilágítanak a gyakorlati szakemberek és az elmélet közötti gyakori módszertani különbözöségekre.

Kérdések, tesztek

1.     Hasonlítsa össze a szisztematikus és nem szisztematikus kockázatot!

2.     Mi a kockázat beárazásának módja a CAPM modellben?

3.     Hogyan lehet mérni az aktívan menedzselt portfóliók teljesítményét?

4.     Mit mutat meg és milyen értékei lehetnek a béta együtthatónak?

5.     Igaz vagy hamis?

a)     Egy értékpapír-portfólió várható hozama az azt alkotó értékpapírok várható hozamának összegével egyenlö

b)     Egy értékpapír-portfólió varianciája az azt alkotó értékpapírok    varianciájának összegével egyenlö

c)      A szisztematikus kockázat diverzifikálható kockázatot jelent

d)     A CAPM modell tökéletesen leírja az értékpapírpiaci árfolyamok alakulását

e)     A Jensen mutató a passzív portfólió teljesítményét méri

Kötelezö és ajánlott szakirodalom

Kötelezö szakirodalom: [1] 166-184.old.

Ajánlott szakirodalom: [2] II., III. fejezet