Pitagorasz-tétele és a pitagoreusok

Pitagorasz-tétele és a pitagoreusok

1.          Pitagorasz életrajza és a pitagoreusok

1.1.Kronológia:

i.e. 570 körül Szamosz szigetén megszületik Pitagorasz

i.e. 530 körül Krotónba érkezik

i.e. 510 Krotón legyözi Szübariszt. A legyözött város sorsa szembeállítja Pitagoraszt a demokratákkal, és emiatt végül a város elhagyására kényszerül.

i.e. 500 körül Pitagorasz meghal Metapontonban

1.2.Kik voltak a pitagoreusok?

Pitagorasz életének i.e. 530-as Krotónba való érkezése elötti eseményeiröl keveset tudunk. Az égei-tengeri Szamosz szigetén született, és vélhetöleg egyiptomi és mezopotámiai utakat tett az ottani bölcseletek é 959g61j s vallások tanulmányozására, ám ezek az utak inkább az öt a tökéletes bölcs vonásával felruházni óhajtó legendák körébe tartoznak. Az viszont bizonyos, hogy i.e. 530-ban Polükratész zsarnoksága elöl menekült a dél-itáliai görög településre, Krotónba, ahol hirdetni kezdte tanait, és rövid idö alatt meg is nyert közel kétezer embert. Ők voltak a pitagoreusok.

1.3.A pitagoreusok felfogása

A pitegoreusok hittek a lélekvándorlásban, vegetáriánusok voltak, és hosszú hajat, és fehér gyapjú köntöst viseltek. Elöször szigorúan elöírt életmóddal és zenével meg kellett lelküket tisztítaniuk. Az így felkészült jelöltek különbözö próbák után léphettek a szövetségbe. Ekkor avatták be öket a számok és a harmónia misztériumába. A számok tudományának a müvelése és a harmóniatanban való elmélyedés biztosította számukra az örök igazság megismerését és az istenséghez való felemelkedést. A pitagoreusoknál a matematikával való foglalkozás vallásos tevékenység volt, amely kiegészítette az életmódbeli elöírásokat. Hittek abban, hogy egy isten van, aki a világot a számok közötti kapcsolatnak, törvényeknek megfelelöen teremtette. Sok szám van ugyan, de mindegyiknek forrása az egység, ugyanúgy a világ sokféle dolgának egyetlen eredete és egységbe foglalója az Isten. A sokféle dolog és jelenség között az isteni harmónia teremt rendet, és az foglalja a mindenséget egységbe, és ez a harmónia ugyanaz, ami a számok tudományában és a zenében is fellelhetö. Az ember igazi hivatása ezeknek a boldogságot biztosító harmóniáknak a megismerése, amihez legeredményesebben a matematika müvelése segíti hozzá. A matematikában, amely az aritmetikát, a geometriát, a csillagászatot és zenét egyesíti, fellelhetök az örök törvények. Ezek biztosítják az ember számára az örökké való istenhez hasonulást, a lélekvándorlástól való megszabadulást, az annyira áhított örök életet.

2.          Pitagorasz matematikai munkássága

Számfilozófiai elméletének hatására Pitagorasz intenzív matematikai kutatómunkát is végzett. Számos tétel kidolgozását tulajdonítjuk neki, ezek között azonban vannak olyanok is, amelyek i. e. 5. századi követöitöl származnak. A derékszögü háromszög oldalainak négyzetéröl szóló, híressé vált Pitagorasz-tételen kívül, a pitagoreusoknak köszönhetjük az arányokról szóló elsö elméletet, a számok osztályozását, az irracionális számok felfedezését, a szorzótáblát és a tízes számrendszert. Amikor felfedezte híres tételét, Pitagorasz hálája jeléül egy ökröt áldozott az isteneknek, de hogy hü maradhasson filozófiai meggyözödéséhez, az ökröt tésztából gyúrták.

A tétel így hangzik:

Egy derékszögü háromszög két befogójának (a, b) négyzetének összege egyenlö az átfogó (c) négyzetével. a²+b²=c²

A tétel, bár Pitagorasz nevét viseli, már az ókorban közismert volt. A New York-i Columbia egyetemen örzik a ma Plimpton 322 néven ismert babiloni táblát. A tábla négy oszlopban és tizenöt sorban elrendezett számokat tartalmaz. Hiányosnak látszik, talán egy nagyobb tábláról tört le. Általánosan elfogadott feltevés szerint a tábla a tört alakú pitagoraszi számhármasok elöállítását mutatja be. A bonyolult eljárás arra utal, hogy a babiloniak már i.e. 1800-1650 körül, azaz több mint ezer évvel Pitagorasz elött ismerték a Pitagorasz-tételt.

3.          Pitagorasz tételének bizonyításai

3.1.    

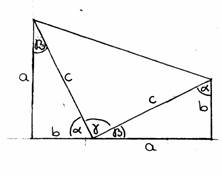
Tekintsük az ábrát! Ezen egy olyan meröleges szárú trapézt látunk, amelynek párhuzamos oldalai a és b, a meröleges szár a+b hosszúságú. A c-vel jelölt szakaszok egyenlöek és merölegesek egymásra. Az egyenlöség nyilvánvaló; a merölegesség pedig azért igaz, mert α+β=90° és γ=180°-(α+β). Számítsuk ki a trapéz területét mint a három háromszög területének összegét! Felírható, hogy T=2 =ab+

Ha pedig azt tekintjük, hogy a trapéz területe a párhuzamos oldalak összege felének és a magasságának a szorzata, akkor

T=(a+b)= +ab.

A két módon kiszámított terület nyilván egyenlö, tehát

ab+ +ab.

Az egyenlet mindkét oldalából ab-t kivonva és 2-vel való szorzás után Pithagorasz tételét kapjuk (c˛=a˛+b˛).

3.2.

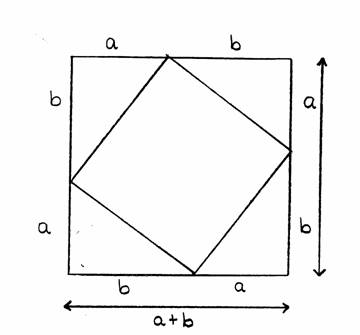
Számítsuk ki az a+b oldalú négyzet területét kétféleképpen. Egyrészt az

(a+b)˛,

másrészt mint a c oldalú négyzet és a négy egybevágó derékszögü területének összege:

c˛+4

Az így számított területek egyenlösége miatt

(a+b)˛=c˛+2ab,

azaz

a˛+2ab+b˛=c˛+2ab,

mindkét oldalból 2ab elvétele után kapjuk, hogy

a˛+b˛=c˛.

A bizonyítás lényege, hogy egy síkidom területét két különbözö módon számítjuk ki.

3.3.

Helyezzünk el négy egybevágó, a, b, c oldalú 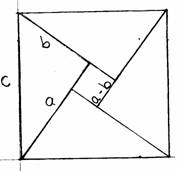derékszögü háromszöget az ábrán látható módon, és legyen a>b. A háromszögek átfogói c oldalú négyzetet határoznak meg, amely a belsejében egy a-b oldalú négytetet tartalmaz. A c oldalú négyzet területe egyenlö a négy egybevágó derékszögü háromszög és az a-b oldalú négyzet területének összegével, vagyis

c˛=4+(a-b)˛,

azaz c˛=2ab+a˛+b˛-2ab, tehát valóban c˛=a˛+b˛.

3.4.

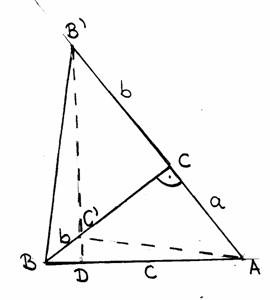
Az ABC háromszög AC=a oldalának c-n túli meghosszabbítására mérjük fel a BC=b oldalt, így kapjuk meg a B' pontot. A BC oldalra pedig C-töl kezdve mérjük az AC=a oldalt, így nyerjük a CC' szakaszt (ábra). Az AB'BC' konkáv négyszög területét fogjuk kétféleképpen kiszámítani. Egyrészt mint a BCB' és AC'C derékszögü egyenlö szárú háromszögek területének összegét: , másrészt mint a BC'B' és AB'C' háromszögek területének összegét. Ez utóbbihoz azonban elöbb be fogjuk bizonyítani, hogy a B'C' egyenes meröleges AB-re és B'C'=AB. Vegyük észre, hogy ha az ABC háromszöget C körül 90°-kal elforgatjuk negatív irányban, B a B'-be, A a C'-be kerül, hiszen ezeket a szakaszokat mértük fel. Az AB szakasz új helyzete tehát B'C' szakasz, ezért B'C'=AB, másrészt pedig 90°-os elforgatással minden egyenes meröleges a saját elforgatottjára, tehát valóban: B'C'┴AB. Így most már könnyü e két utóbbi háromszög területét kiszámítani. A BC'B' háromszög alapjának vegyük a B'C' oldalt, akkor magassága BD, az AB'C' háromszögnek pedig a B'C' alaphoz tartozó magassága DA, ahol BD+DA=BA, tehát e két háromszög területösszege

+ , s így , amiböl Pitagorasz tétele következik (mindkét oldalt elosztom 2-vel).

3.5. b a b a

a c a T₁ a a b

c c

b a

T₂

b T₂ bbb

a

ba a b

abab ab

4 +b²+a²⁼4a +c^{2 4}

2 2 2

a²+b²=c²

3.6.

a

b                          a

c

T₁        b

T₂

c                    b

Ta a

b    a

Tb

T₁ = a×a = a²

T₂ = b×b = b²

T₁+T₂ = a²+b² = c2, mert az alap háromszög és a c-re emelt négyzetben lévö háromszög egybevágó.

4. Érdekességek

4.1. Pitagorasz tételének megfordítása és ennek bizonyítása

Ha egy háromszög két oldalára emelt négyzetek területe egyenlö a harmadik oldalra emelt négyzet területével, akkor a háromszög derékszögü.
Legyen adott egy ABC háromszög, amelynek oldalaira teljesül, hogy két oldalára emelt négyzetek területe egyenlö a harmadik oldalra emelt négyzet területével.

A mellékelt ábra jelölései szerint:

a² + b² = c².

Be kell bizonyítani, hogy az ABC háromszög derékszögü.

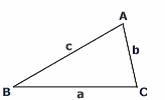
Vegyünk fel egy "a" és "b" befogójú derékszögü háromszöget. Ennek átfogóját jelöljük "c'"-vel. Erre a háromszögre teljesül a Pitagorasz-tétel, tehát:

a² + b² = c².

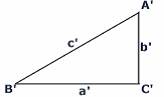
A két összefüggés csak akkor lehet egyszerre igaz, ha c² = c'². Ez viszont azt jelenti, hogy a két háromszög egybevágó, tehát az eredeti ABC háromszög is derékszögü.

4.2. A pitagoraszi számhármasok

A pitagoraszi számhármasok azok a lehetséges a,b,c oldalakra vonatkozó egész arányszámok, amelyek esetén a Pitagorasz-tétel igaz. A pitagoraszi számhármasok végtelen számú gyártásának a módszere a pitagoreusokhoz kötödik.

Írjuk egy sorba négyzetszámokat, alá pedig a páratlan számokat. Így minden alsó sorban lévö számhoz kettö fog tartozni a felsö sorból, és ezek együtt alkotnak egy számhármast.

1 4 9 16      25 36 49 64 81 100
1 3 5 7 9 11 13 15 17 19

A legkisebb számhármas tehát a 3,4,5.

5.          Irodalomjegyzék

1.       Breznai Gyula: Pitagorasz tétele (Tankönyvkiadó Budapest, 1971-1972)

2.       Larousse Panteon I. - A kezdetektöl a középkorig (szerk. felelös szerkesztök: Carl Anderhold, Jannie Faure, Laure Talamon, Christiane Oschner; szerkesztette: Nagy Mézes Rita, Kossuth Kiadó, Budapest, 2002)

3.       K. A. Ribnyikov: A matematika története (Tankönyvkiadó, Budapest, 1968)

4.       Sain Márton: Nincs királyi út! (Gondolat, Budapest, 1986)

5.       Sain Márton: Matematikatörténeti ABC (tankönyvkiadó, Budapest, 1973-1974)

6.       Richard Mankiewicz: A matematika históriája (HVG Kiadói RT. - HVG könyvek, Budapest, 2003)