Diszkrét valószínüségi változók együttes és peremeloszlása

Adott Q eseménytér két valószínüségi változója kapcsolatát azok együttes eloszlásával írhatjuk le. A  p_ij = P(x=x_i, h=y_j) (i=1...n, j=1..m) valószínüségek összességét x és h együttes eloszlásának nevezzük.

Peremeloszlás

Táblázatban ábrázolva x és h együttes eloszlását, az egyes x_i, y_j valószínüségeket soronként, illetve oszloponként összesíthetjük. Az így kapott összesített valószínüségeket nevezzük x-re, illetve h-ra vonatkozó marginális eloszlás 717e43h oknak, más néven peremeloszlásoknak:

A (x h)-nak a x-hez tartozó peremeloszlása pontosan azt mutatja meg, hogy mekkora valószínüséggel veszi fel a x az x_i értékét, függetlenül attól, hogy az h milyen értéke valósul meg. Hasonló meggondolással jutunk a h eloszlásának meghatározására is. Tehát

és .

Nyilvánvaló, hogy a p_ij együttes eloszlás teljesíti az alábbi feltételt:

Feltételes eloszlások

A x valószínüségi változó h = y_i feltételre vonatkozó feltételes valószínüség-eloszlása az alábbi képlettel adható meg:

P(x = x_i | h = y_i) =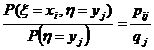, i = 1,2,.

Hasonlóképpen értelmezzük az h = y_j esemény x = x_i feltétel melletti valószínüségét is:

P(h = y_i | x = x_i) =, j = 1,2,.

Változók függetlensége

x és h valószínüségi változók akkor függetlenek, ha a vizsgálatba vont minden elemre teljesül az alábbi összefüggés:

p_ij = p_i*q_j

azaz együttes valószínüségük a változók minden értékénél megegyezik a megfelelö sor és oszlop szerinti peremeloszlások szorzatával.

Illetve, ha:

Folytonos valószínüségi változók együttes és peremeloszlása

Ha a (x h) valószínüségi változópárban a x és h is folytonos változó, akkor együttes eloszlásukat egy eloszlásfüggvénnyel (ill. sürüségfüggvénnyel) adjuk meg.

A H(x,y) = P(x, < x, h < y) kétváltozós függvényt a kétdimenziós (x h) valószínüségi vektorváltozó kétdimenziós eloszlásfüggvényének, vagy a x és h valószínüségi változók együttes eloszlásának nevezzük.

A függvény tulajdonságai megegyeznek az egydimenziós eloszlásfüggvény tulajdonságaival:

H(x,y) mindkét változója szerint monoton növekvö,

, , ,

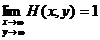H(x,y) mindkét változója szerint balról folytonos.

Peremeloszlás

A kétdimenziós eloszlásokból a

és a szabállyal származtatott F(x) és G(y) egydimenziós eloszlásokat peremeloszlásoknak nevezzük.

Együttes sürüségfüggvény

A sürüségfüggvény az eloszlásfüggvény másodrendü parciális deriváltja. Tehát

és .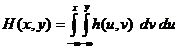

A sürüségfüggvény tulajdonságai

h(x,y) < x < - < y <

,

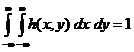P(a x < b; c h < d) =.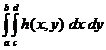

Perem-sürüségfüggvények

A x változó sürüségfüggvénye: .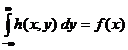

A h változó sürüségfüggvénye: .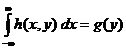

Feltételes eloszlások

A x folytonos valószínüségi változó h = y feltételre vonatkozó feltételes sürüségfüggvényén az

f(x | y) = függvényt értjük.

Hasonlóan

g(y | x) =.

A sürüségfüggvény az eloszlásfüggvény parciális deriváltja.

A x valószínüségi változó h = y feltételre vonatkoztatott feltételes eloszlásfüggvényét az

F(x | y) = P(x x | h = y)

egyenlöséggel definiáljuk. Hasonlóan definiálhatjuk az h változónak a x = x feltételre vonatkozó feltételes eloszlásfüggvényét:

G(y | x) = P(h y | x = x)

Változók függetlensége

A x és h valószínüségi változókat függetlennek tekintjük, ha együttes eloszlásfüggvényük egyenlö perem-eloszlásfüggvényük szorzatával, ill. sürüségfüggvényük egyenlö perem-sürüségfüggvényük szorzatával.

H(x,y) = F(x)G(y) és h(x,y) = f(x)g(y)

Korrelációs együttható

Q eseménytérben felvett x és h valószínüségi változók közötti kapcsolat általában nem írható le függvénnyel, mert a változók között sztochasztikus kapcsolat van. Ennek a kapcsolatnak a szorosságát mérhetjük a kovariancia, illetve a korrelációs együttható segítségével.

Kovariancia

A kovarianciát úgy definiálhatjuk, mint x és h változók súlyozott átlagtól való eltérései szorzatának várható értékét:

cov(x h) = M((x - M(x h - M(h

Egyszerübb alakban:

cov(x h) = M(xh) - M(x)*M(h

A kovariancia tulajdonságai

Szimmetria: cov(x h) = cov(h x

|cov(x h D(x)*D(h

Korrelációs együttható

A kovariancia nagyságát jelentösen befolyásolja a valószínüségi változók értékeinek nagyságrendje, így számszerü értéke önmagában nem jellemzö a két változó közötti kapcsolat szorosságára. A korrelációs együttható értékét úgy kapjuk, ha a kovarianciát egységnyi szórásra normalizáljuk, azaz értékét elosztjuk a két változó szórásának szorzatával:

A korrelációs együttható tulajdonságai

|R(x h

Az |R(x h akkor és csak akkor egyenlö 1-gyel, ha x és h között lineáris kapcsolat áll fenn, azaz, ha létezik olyan a <> 0 és b szám, hogy h = ax + b. Ebben az esetben R(x h = 1, ha a > 0, és R(x h = -1, ha a < 0.;

Ha a x és h valószínüségi változók függetlenek, akkor R(x h

Ha R(x h = 0, akkor ebböl nem következik, hogy a valószínüségi változók függetlenek. Ilyenkor azt mondjuk, hogy a valószínüségi változók korrelálatlanok. Ez azt jelenti, hogy az M(xh) = M(x)*M(h egyenlöség fennáll.

Ha x és h korrelálatlanok és létezik a szórásuk, akkor D²(x h) = D²(x)+D²(h