Letöltheto dokumentumok, programok, törvények, tervezetek, javaslatok, egyéb hasznos információk, receptek - Fájl kiterjesztések - fajltube.com

  51. ábra Höenergia-átadása exoterm és endoterm kémiai reakciókban

Belsö energia

A termodinamikai rendszer teljes energiakészletét belsö energiának hívjuk. A belsö energia a rendszert alkotó molekulák haladó, forgó és rezgö mozgásának, a molekulán belüli atomok mozgásának és az alkotórészek közötti kölcsönhatási energiáknak az összege. Nem tartoznak a belsö energiába a test egészének mozgásával és helyzetével kapcsolatos mechanikai energiák (kinetikus és helyzeti energia). A belsö energia függ a rendszer anyagi minöségétöl és állapotától. A rendszer belsö energiáját mérni ugyan nem lehet, de a belsö energia változásokat (DE) tudjuk mérni vagy számítani, ami megfelel a végállapot és a kezdeti állapot belsö energiája különbségének:

DE = E_végállapot - E_{kezdeti állapot}

A belsö energia növekszik a kémiai rendszerben:

* a hömérséklet emelésével (pl. nagyobb lesz a gázmolekulák kinetikus energiája);

*szilárd folyadék, folyadék gáz átalakuláskor (olvadás, párolgás során), mert a fázisátmenetekhez energiabefektetés szükséges az intermolekuláris erök legyözéséhez;

*a kémiai reakció lejátszódását a belsö energia fedezi; a belsö energia növekedésekor a kémiai kötések felbomlanak, míg újak kialakulásakor a belsö energia csökken. Endoterm reakcióban a rendszer a környezetétöl veszi fel a szükséges energiát.

Hütéskor, fagyás vagy kondenzáció során a rendszer belsö energiája csökkenhet. A belsö energia növelése csak ritkán indít el kémiai reakciókat; gyakoriak azonban az olyan reakciók amelyeknél a belsö energia összességében csökken.

A termodinamika I. fötétele

A legsarkalatosabb természettudományos felismerések közé tartozik az energiamegmaradás törvénye (Mayer, 1842; Joule, 1843), mely szerint az energiafajták átalakíthatók ugyan egymásba, de energiát semmiböl nem lehet teremteni, viszont nem is lehet megsemmisíteni. Késöbb ugyan kiderült, hogy az energia és a tömeg nem függetlenek egymástól (DE = c² . Dm; Einstein, 1905), de a klasszikus fizika tárgykörébe esö történések és a kémiai folyamatok vonatkozásában ennek nincs jelentösége.

Az energiamegmaradás törvényével szoros összhangban van a termodinamika I. fötétele, melynek értelmében egy termodinamikai rendszer belsö energiájának megváltozása (DE) a rendszer által felvett vagy leadott höenergia (Q) és a rendszeren, vagy a rendszer által végzett munka (W) algebrai összegével egyenlö:

DE = Q + W.

A termodinamika I. fötétele tehát kimondja, hogy zárt rendszerben a belsö energia változását a rendszer és a környezete közötti höcsere, valamint a munka határozza meg. Az egyenletben szereplö mennyiségek elöjelét önkényesen meghatározva a DE pozitív, ha a rendszer energiát vesz fel, és negatív ha energiát ad le. Pozitív elöjelü a környezetböl felvett hö, ill. a környezet által a rendszeren végzett munka; negatív elöjelü a rendszerböl a környezetének leadott hö, ill. a rendszer munkavégzése a környezettel szemben (egocentrikus elöjel-konvenció).

A termodinamikai folyamatokat (köztük a kémiai folyamatokat is) igen gyakran térfogatváltozás (DV) kíséri. Az ezzel együtt járó munka, az un. térfogati munka (W_térf), mely állandó nyomáson (P) és hömérsékleten:

W_térf = - Pˇ DV.

Térfogatnövekedés esetén a térfogati munka elöjele negatív, mert a rendszer végez munkát; térfogatcsökkenéskor a térfogati munka pozitív elöjelü, mert a külsö nyomás végez munkát a rendszeren. A nyílt rendszerekben lejátszódó térfogati munka semmire sem használható, ezért célszerü ezt megkülönböztetni az egyéb jellegü munkától, mely elvileg tetszés szerint hasznosítható (W_h). Ezek szerint:

W = W_térf + W_h.

Olyan folyamatoknál, amelyeknél nincs térfogati munka (DV=0) és egyéb munkavégzés sem történik (W=0), a belsö energiaváltozást csak a rendszer és a környezete közötti höcsere határozza meg: DE = Q_v, ahol Q_v az állandó térfogaton mért hökicserélödés.

Entalpia

Az elözöek szerint nyílt rendszerekben állandó nyomáson végbemenö térfogati munka gyakorlati szempontból érdektelen, s így legtöbbször felesleges azt külön is számításba venni. Lényegében ez a megfontolás vezetett el az entalpia fogalmához.

Ha a folyamat hasznos munka végzése nélkül, állandó nyomáson, de térfogatváltozás közben játszódik le, a rendszer belsö energiájának változása:

DE = Q_p - PˇDV ,

ahol Q_p az állandó nyomáson mért reakcióhö,

a -PˇDV pedig a térfogati munkát jelöli. Az egyenlet átrendezve:

Q_p = DE + PˇDV ,

Az egyenlet jobb oldalát képezö összeg (DE + PˇDV) definíciószerüen a rendszer entalpiája megváltozását jelenti. Ennek szokványos jelölése (DH), így az entalpia megváltozása:

DH = DE + PˇDV.

Ennek megfelelöen a termodinamika I. fötétele állandó nyomáson:

DH = Q_p.

Térfogatváltozással járó reakciókban a reakcióhö az entalpiaváltozással azonos. Az entalpia az anyagok hötartalmát jelenti állandó nyomáson; a belsö energia, a nyomás és a térfogat függvénye:

H = E + PˇV.

A belsö energiához hasonlóan függ a rendszer anyagi minöségétöl és állapotától. A kémiai reakció entalpiaváltozása a termékek entalpiájának összege és a kiindulási anyagok entalpiájának összege közti különbséggel egyenlö:

DH = SH_termékek -SH_{kiindulási anyagok}.

Az entalpia állapotfüggvény és extenzív mennyiség; mértékegysége a joule. Változása állandó térfogaton lejátszódó folyamatok esetén a belsö energia megváltozásával egyenlö, vagyis

DH = DE,         ha DV = 0.

Gyakorlati szempontból sokkal inkább érdekelnek bennünket az állandó nyomáson lejátszódó folyamatok. Az ezeket kísérö höváltozásokat entalpia-különbségekként lehet leírni, így az entalpiát hötartalomnak is nevezhetjük.

A párolgáshö az a hömennyiség, amely 1 mól folyadék gözzé alakításához szükséges állandó nyomáson és adott hömérsékleten. Ez az entalpia segítségével felírva:

DH_párolgás = H_göz - H_folyadék.

A párolgással fordított irányú folyamat a kondenzáció, s az annak megfelelö höváltozás:

DH_{kondenzáció} = H_folyadék - H_göz.

Mivel H_göz > H_folyadék

DH_párolgás > 0, vagyis a párolgás endoterm folyamat, és

DH_{kondenzáció} < 0, vagyis a kondenzáció exoterm.

Az elözö két egyenletböl az is látható, hogy DH_párolgás DH_{kondenzáció}, ami az energiamegmaradás törvényének egyenes következménye. A párolgáshö és a kondenzációshö önkényesen kiragadott példákat jelentenek, hiszen ugyanilyen viszonyban áll egymással pl. az olvadás- és a fagyáshö, továbbá a szublimációs- és a lecsapódási hö is.

A hökapacitás és a fajhö fogalma, valamint az entalpia hömérsékletfüggése

A hökapacitás az a hömennyiség, amely a rendszer hömérsékletét 1 K-el emeli anélkül, hogy abban belsö átalakulás (halmazállapot-változás, kémiai reakció) következne be. Jele C_P vagy egyszerüen csak C, ha höfelvétel közben nyomásváltozás nem történik, és C_V, ha a folyamat nem jár együtt térfogatváltozással. Mértékegysége: J K^-1.

Fajhö alatt az 1 kg tömegü anyag hökapacitását értjük. Jele az elöbbi értelmezés szerint c_p, c vagy c_v, mértékegysége J kg^-1 K^{-1. Ha a hökapacitást nem a tömegegységre, hanem az anyagmennyiségre vonatkoztatjuk, akkor az ún. moláris hökapacitást kapjuk. A moláris hökapacitás tehát a fajhövel és nem a hökapacitással analóg fogalom.}

Ha nincs halmazállapot ill. módosulatváltozás, és kémiai reakció sem játszódik le a rendszerben, DT hömérsékletváltozás hatására az alábbi entalpiaváltozás következik be:

DH n C_P (T₂-T₁) n C_P DT,

ahol n az anyagmennyiség (mol), C_P az állandó nyomáson mért moláris hökapacitás (J K^-1 mol^-1), T₂ és T₁ pedig a                              végállapot és a kezdeti állapot termodinamikhömérséklete (K).

A kémiai és fizikai folyamatok entalpiaváltozása

A folyamatok egyensúlyra jutása termodinamikailag azt jelenti, hogy a kémiai összetételben megszünnek a változások, és a rendszer hömérséklete ismét azonos lesz a környezetével. A folyamatokat kísérö höváltozásokat a reakcióhö fejezi ki, ami állandó nyomáson egyenlö az entalpiaváltozással.

Exoterm reakciókban a DH negatív, mivel entalpiacsökkenés játszódott le; endoterm reakciókban pedig a DH pozitív, mivel a folyamat entalpianövekedéssel jár.

A termokémiai egyenletekben a reakcióhöt is feltüntetjük, így pl. a foszfor-triklorid képzödése:

P(s) + 3/2 Cl₂(g) = PCl₃(l) DH = -319,7 kJ

exoterm folyamat, mert 1 mól foszfor reakciója másfél mól klórgázzal entalpiacsökkenéssel jár; a termék entalpiája kisebb, mint a kiindulási anyagoké.

Ezzel szemben a higany-oxid bomlása elemeire, endoterm folyamat, mert a termékek entalpiája nagyobb, mint a kiindulási anyagé:

2 HgO(s) =2 Hg(l) + O₂(g) DH = +181,7 kJ.

A kémiai reakciók entalpiaváltozásának megismeréséhez nem szükséges ismernünk a részvevö anyagok abszolút entalpiáját. Szükség van azonban egy vonatkoztatási alapra, a standardállapotra, amelyhez viszonyítani tudjuk az entalpiaváltozásokat. A standardállapot az elemek és vegyületek legstabilabb fizikai formáját jelenti 0,1 MPa nyomáson és 298 K-on. A standardentalpia-változás (DH^o) azt az entalpiaváltozást jelenti, amikor a kiindulási anyagok és a termékek is standardállapotban vannak.

Képzödési entalpiák

A standardállapotban lévö elemek entalpiája megállapodás szerint nulla. Azt az entalpiaváltozást, amely akkor lép fel, amikor a standardállapotú vegyület 1 mólja standardállapotú elemekböl képzödik, a vegyület standard képzödési entalpiájának nevezzük (). A víz képzödésének standard képzödési entalpiája:

H₂(g) + 1/2 O₂(g) =H₂O(l) = -285,8 kJ,

ahol a H₂ és O₂ gáz, a H₂O pedig folyékony halmazállapotban szerepel, mivel 0,1 MPa nyomáson és 298 K-en ezek a formák stabilak. Néhány anyag képzödési entalpiája a 27. táblázatban látható.

27. táblázat. Standard képzödési entalpiák

A vegyületek alkotóelemeire való bomlásakor az entalpiaváltozás abszolút értéke ugyanakkora, mint a képzödési entalpia, de azzal ellentétes elöjelü.

Reakcióhö

A reakcióhö a kémiai reakciókat kísérö höváltozás (kJ/mol), vagyis a megfelelö reakcióegyenlet szerinti végtermékek és a kiindulási anyagok entalpiaösszegének különbsége. Egy reakció standard entalpiaváltozását a termékek és a kiindulási anyagok képzödési entalpiája különbségéböl számíthatjuk ki:

DH_r = SH _{végtermékek} - SH_{kiindulási anyagok}

A reakcióhö természetesen attól is függ, hogy a végtermékek és a kiindulási anyagok milyen fizikai állapotban vannak. Ha ez mindkét esetben 25 ^oC és 0.1 MPa, standard reakcióhöröl () van szó. Ez utóbbi kiszámítható pl. olymódon, hogy a végtermékek képzödéshöinek összegéböl kivonjuk a kiindulási anyagok képzödéshöinek összegét:

= S - S.

Égéshö

Bizonyos kémiai folyamatok esetében a kísérö entalpiaváltozást külön névvel is ellátták; ezek közé tartozik pl. a közömbösítési hö és az égéshö. Az oxigénnel való egyesülés rendkívül nagy fontossága miatt (fosszilis energiahordozók felhasználása, biológiai oxidáció) az utóbbi bevezetése különösen indokolt.

A kémiában égéshö alatt általában az 1 mól anyag oxigénfeleslegben való tökéletes elégetésekor felszabaduló hömennyiséget értjük; egysége kJ/mol. A nem meghatározott összetételü anyagok égéshöjét (fa, köszén, élelmiszer) kJ/kg, ill. kJ/m³ egységben szokás megadni. (A tüzelöanyagok fütöértéke mindig kisebb, mint az égéshö, mert az égés során felszabaduló hönek bizonyos része a fütöberendezés korlátozott hatásfokától eltekintve is kárba vész, mert höt igényel pl. a tüzelöanyag nedvességének felmelegítése és elpárologtatása.)

Az égéshö az ún. kaloriméter segítségével megfelelö pontossággal meghatározható. Ez többek között azért nagy jelentöségü, mert lehetöséget nyújt az élelmiszerek hasznosítható energiatartalmának becsléséhez. Ennek elvi alapját a Hess-törvény képezi.

28. táblázat. Néhány vegyület és tápanyag égéshöje

A 31. táblázat néhány anyag égéshöjét mutatja kJ/g-ban. A táblázat adataiból látható, hogy a hidrogén égéshöje a legnagyobb, ezért a hidrogénben gazdag szénvegyületek égéshöje (metán, acetilén, trigliceridek) nagyobb, mint az oxigént is tartalmazó szénvegyületeké (poliszacharidok, cukrok, ecetsav, etilalkohol). A szénhidrátok és a zsírok szervezetben történö "égése" a kémiai égéshövel majdnem azonos entalpiaváltozással jár. Ennek az a magyarázata, hogy a szénhidrátok és a zsírok szén-dioxiddá és vízzé oxidálódnak, mind a szervezetben, mind a kémiai égés során. A nitrogéntartalmú tápanyagok esetén az élettanilag hasznosítható energiaérték kisebb mint a kémiai, mivel a nitrogén csak részben oxidálódik, és a szervezetböl a madaraknál húgysav, az emlösöknél pedig karbamid formájában ürül ki.

Hess tétele

Hess tétele értelmében a reakcióhö értéke csak a folyamat kezdeti és végállapotától függ, és nem függ attól az úttól, amelyen a változás végbemegy. Hess tétele összhangban van az energiamegmaradás törvényével; segítségével a folyamatok entalpiaváltozása kiszámítható. Az elözöek értelmében a szén oxigénnel való egyesülésekor az entalpiaváltozás ugyanakkora, akár közvetlenül történik az égés:

C(s) + O₂(g) = CO₂(g) DH^o = -393,5 kJ,

akár két lépésben:

C(s) + 1/2 O₂(g) = CO(g) = -110,5 kJ

CO(g) + 1/2 O₂(g) = CO₂(g) = -283,0 kJ

C(s)+ 1/2 O₂ (g) CO (g) +1/2 O₂ (g) = CO (g) + CO₂(g)

DH^o = + = -393,5 kJ

Energiadiagram alapján a 52. ábra mutatja.

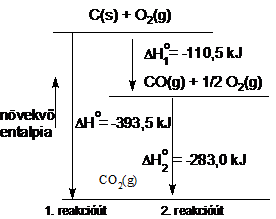
52. ábra. Hess tétele. A szén égetése szén-dioxid gázzá

Hess tétele alapján az élelmiszerek kalorimetrálással meghatározott égéshöje támpontot ad a biológiai égés energiatermelésére. A vizsgált anyagban lévö hidrogén és szén esetében az összehasonlíthatóság többé-kevésbé megvan, mivel az oxidációs végtermék mind a kaloriméterben, mind a szervezetben víz és széndioxid. Problematikus azonban ebböl a szempontból, mint az ahogy már említésre került, a nitrogén (aminosavak), mivel az a kalorimetrálás végén nitrogén gáz formában jelenik meg, a szervezetböl viszont karbamid (NH₂-CO-NH₂) formában távozik a vizelettel.

Kötési energiák

A kötési energia annak az 1 mólnyi anyagra vonatkoztatott energiának az átlagértéke, amely adott típusú kémiai kötés felbontásához szükséges. Egy másik értelmezés szerint azt az energiát tekintjük kötési energiának, amely felszabadul, ha egymástól nagy távolságra lévö atomok az adott kötéstípussal egyesülnek. A kötési energiákat az abban résztvevö atomok minösége szabja meg. Kettönél több atomos molekulákban azonban a többi atom minösége, valamint a kötés molekulán belüli helye is befolyásolja a kötési energiát. Ezért a kötési energiák mellett általában az átlagos jelzöt szoktuk használni.

A kötési energiák az illetö anyag egyéb termokémiai adataiból (pl. égéshö) számítható ki a Hess-tétel figyelembevételével.

A hidrogén és a klór kötési energiáját az alábbiak mutatják:

H₂(g) = 2 H(g) DH^o = -435 kJ,

Cl₂(g) = 2 Cl(g) DH^o = -243 kJ.

Mindkét reakcióban a kétatomos molekula 1 mólnyi kötése szabadul fel (6,0226ˇ10²³ kötés); a kötési energia az 1 mólnyi anyagban lévö adott típusú kötés képzödéshöjének felel meg. A kovalens kötések kötési energiái negatív elöjelüek, ami egyrészt utal az exoterm höváltozásokra, másrészt összhangban van azzal, hogy a molekulák képzödése a belsö energia ill. entalpia csökkenésével jár.

Összetettebb szerkezetü molekuláknál a kötési energiákat önkényesen rendeljük az egyes kötésekhez. Egy bizonyos kötéstípus felszakításához szükséges energia közelítöleg azonos, függetlenül attól, hogy milyen molekulában található. Így pl. a C-H kötés erösségét azonosnak tekintjük, függetlenül attól, hogy szénhidrogénben, szénhidrátban vagy fehérjében fordul elö, ezért a táblázatban megadott kötési energiák átlagos kötésü energiák, mivel a számítás során feltételezték, hogy a molekulában szereplö azonos típusú kovalens kötés energiája azonos. A valóságban azonban a többatomos molekulák disszociációjakor a C-H kötések felbontása egyenként történik, ezért az elsö kötés energiája nagyobb pl. a metánban mint a másodiké, az nagyobb mint a harmadiké, és az nagyobb mint a negyediké. A kötési energiák additivitása lehetövé teszi a molekula képzödési höjének kiszámítását is. A számított képzödési hö és az égéshökböl kísérletileg meghatározott képzödési hö összehasonlításával a molekulaszerkezetre lehetett következtetni.

A fizikai folyamatok entalpiaváltozása

Az energiamegmaradás törvényéböl következik, hogy a halmazállapot-változásokat kísérö entalpiaváltozások abszolút értéke független a folyamat irányától, hogy pl. szilárd halmazállapotból folyékony keletkezik, vagy folyékony halmazállapotból szilárd. Az ellentétes folyamatok, pl. olvadás-fagyás entalpiaváltozásai megegyeznek, az olvadás azonban endoterm, a fagyás pedig exoterm folyamat. Hess tételével megegyezöen a szublimációhö értéke az olvadáshö és a párolgáshö összege.

Az ionos vegyületek oldását exoterm vagy endoterm höváltozás kíséri. Az oldandó anyag részecskéi közötti vonzóeröt energiabefektetéssel lehet legyözni, míg az oldószer és az oldandó anyag között új kölcsönhatások alakulnak ki, ami energiafelszabadulással jár. A két folyamat energiaváltozásának viszonylagos nagysága szabja meg, hogy a folyamat exoterm vagy endoterm.

Az oldáshö az a hömennyiség (DH_oldás), amely elnyelödik vagy felszabadul, ha 1 mól anyagból oldószer felhasználásával híg oldatot készítünk. Az oldáshö a kristályrács szétrombolásához szükséges rácsenergia (H_rács> 0) és az ún. szolvatációshö (H_{szolvatáció}< 0) algebrai összegeként értelmezhetö. A szolvatációs hö az a höenergia, amely az oldatba került részecskék szolvátburkának kialakulásakor felszabadul. Ha az oldószer víz, a kialakuló szolvátburok és így a szolvatációhö hidrátburoknak és hidratációhönek is nevezhetö. Fentiek szerint:

DH_oldás DH_rács + DH_{szolvatáció}.

Ha DH_rács > DH_{szolvatáció}, akkor DH_oldás > 0, vagyis a folyamat endoterm,

Ha DH_rács < DH_{szolvatáció}, akkor DH_oldás < 0, vagyis a folyamat exoterm.

A kálium-klorid ionjainak disszociációjához szükséges energia pl. azonos - bár ellenkezö elöjellel - a kristály kialakítását kísérö entalpiaváltozással. A disszociáció mindig endoterm folyamat:

KCl(s) = K⁺(g) + Cl (g)                    DH^o = 701 kJ.

Az oldás második lépése, a szabad ionok hidratációja, exoterm reakció:

K⁺(g) + Cl (g) =   K⁺(aq) + Cl (aq) DH^o = -685 kJ.

Az endoterm disszociáció és az exoterm hidratáció együttesen adja a KCl 1 móljának oldáshöjét:

KCl(s) = K⁺(aq) + Cl (aq) DH^o = 16 kJ.

A NaCl oldáshöje endoterm (3,9 kJ/mol), a LiCl oldáshöje pedig pl. exoterm (-37,2 kJ/mol).

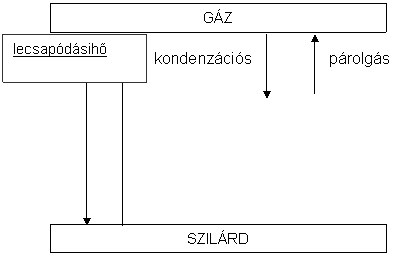
növekvö

szublimáci-óshö

entalpia

FOLYÉKONY

53. ábra. A halmazállapot-változásokat kísérö entalpiaváltozások áttekintése

Az entrópia és a termodinamika II. fötétele

A kémiai folyamatok a valóságban határozott irányban önként mennek végbe, megfordításuk csak energia-befektetéssel történhet. A termodinamikában az ''önként'' kifejezés a folyamat külsö hatástól mentes lejátszódását, az egyensúly felé való irányulását jelenti. Az önként végbemenö változás megmutatja az irányt, de nem ad információt a reakció lejátszódási idejéröl. A termodinamikailag önként végbemenö folyamatok így nagyon gyorsan és igen lassan is végbemehetnek. A termodinamika I. fötétele csak a teljes energiaváltozást írja le, de nem teszi lehetövé a folyamatok irányának megjósolását.

A kémiai és fizikai folyamatokat az entalpiaváltozás mellett egyéb változások is kísérik. A gázfejlödéssel járó reakciókban az egyik termék gázfázisba lép, és ezzel molekulái számára nagyobb mozgási lehetöség nyílik meg.

Ezzel ellentétben a csapadékképzödéssel járó reakciókban a hidratált ionok mozgása jelentösen csökken, mivel azok a kristályrácsban jobban rögzítettek, mint a vizes fázisban. A gázfejlödéssel és a csapadékképzödéssel járó folyamatban megváltozott a kémiai rendszer rendezettsége; az elsö esetben a rendezetlenség, a második esetben a rendezettség növekedett. Hasonló változásokkal járnak a fizikai folyamatok is; a víz párolgásakor a göztérbe kerülö molekulák nagyobb mozgási szabadsággal járó állapotba kerülnek, tehát a rendszer rendezetlensége növekszik.

Bármely makroszkopikus rendszer esetében a rendszer adott állapotát (pl. energia eloszlását) csak statisztikai átlagban lehet bemutatni. Az átlagértéket leíró makro állapotot a rendszert alkotó atomok vagy molekulák nagyon sokféle mikro állapota alakíthatja ki. A termodinamika ezért statisztikus jellegü is; eredményei értelmezésében jelentös szerepe van a különbözö állapotok egymástól eltérö valószínüségének. A termodinamikai valószínüség azon mikro állapotok száma, amelyekkel a rendszer adott makro állapota megvalósul. Kevésbé valószínü a nagyfokú rendezettség, míg sokkal valószínübb a rendezetlenség. Egy makroszkopikus anyagi rendszer adott állapotának valószínüségét, ill. a rendezetlenség mértékét az entrópia (S) fejezi ki. A folyamatot kísérö entrópia változás:

DS = S _végállapot - S _{kezdeti állapot}.

Minden olyan folyamat, mely növeli a rendszeren belüli mozgások lehetöségét (disszociáció, párolgás, olvadás), az adott struktúra felbomlása, vagyis a rendezetlenség irányába hat, azaz entrópia növekedést eredményez. Az entrópia extenzív sajátság és állapotfüggvény. Mértékegysége: J/K. Az entrópiát közvetlenül mérni nem lehet. Boltzmann javasolta elöször az entrópia és a valószínüség összekapcsolását. Az entrópia statisztikus leírásában bevezetett termodinamikai valószínüség (Z, melynek értéke 1 és a között van) a rendszer mikro állapotait viszonyítja a makro állapothoz.

Boltzmann egyenlete az entrópiáról:

S = kˇlnZ,

ahol k a Boltzmann-féle állandó,

Z pedig a termodinamikai valószínüség.

Tökéletesen rendezett állapotban Z=1 és ekkor S=0. Környezetétöl elszigetelt rendszerben az entrópia az önként végbemenö folyamatokban nö, mivel a rendezetlen állapot a valószínübb. Maxwell gondolat-kísérletében kimutatta, hogy ha az önként végbemenö folyamatokban az entrópia csökkenne, azaz a rendezettség nöne, akkor a rendszer hasznos munkát végezhetne energiabefektetés nélkül.

A termodinamika II. fötétele

A rendszer és környezetének entrópiája önként végbemenö folyamatokban állandóan nö, azaz:

DS_rendszer + DS_környezet > 0.

Az egyenlet alapján a rendszerben spontán entrópia csökkenés is lejátszódhat, amit azonban a környezet nagyobb entrópia növekedése ellensúlyoz; így összességében növekszik az entrópia. Az önként végbemenö folyamatok irányát az entrópia növekedés (nyílt rendszereknél)

DG = DH - Tˇ DS < 0 feltétel érvényesülése) szabja meg.

Néhány példa az entrópia növekedésre önként lejátszódó folyamatokban:

*Gázok kiterjedése állandó hömérsékleten növeli a rendezetlenséget, mivel a molekulák mozgása nagyobb térben valósulhat meg.

*Folyadékok forrása során a hömérséklet emelésével ugrásszerüen nö a rendezetlenség.

*Keverés során a részecskék változatosabban helyezkednek el. Azonos hömérsékletü és nyomású gázok elegyítése csak entrópia növekedéssel jár, az entalpia változatlanul maradása mellett.

Az abszolút entrópia

A belsö energia (entalpia) abszolút értékét nem lehet meghatározni, csak változása mérhetö. Ezzel szemben a rendszer rendezetlensége, entrópiája jól nyomon követhetö. A hömérséklet csökkenésével a tiszta anyagok részecskéinek mozgási lehetösége csökken, és megfelelöen alacsony hömérsékleten szilárd halmazállapotba kerül, majd 0 K-on megszünne a kristályt alkotó atomok rezgö mozgása is. Amennyiben tökéletes kristály alakulna ki, ahol minden atom állapota azonos, a makroállapot egyetlen mikroállapottal valósulna meg, ezért a tökéletes kristály entrópiája T = 0 K hömérsékleten nulla. Ebböl következik az is, hogy az abszolút 0 pontot megközelíteni lehet, de elérni soha. Reális kristályok entrópiája nagyobb mint nulla T = 0 K-on, mert a részecskék a rácshibák és a többféle orientáció miatt változatosan helyezkedhetnek el a térben. Egy anyag abszolút entrópiája egy adott hömérsékleten az alábbi entrópiákból számolható:

*T = 0 K-on számított entrópia, amely függ a molekula geometriájától és a kristályrács szerkezetétöl.

*A fázisátmenetek során bekövetkezö ugrásszerü entrópia növekedés.

*A fázisokban lejátszódó hömérséklet-növekedés, mely növeli az entrópia értékét.

Az abszolút entrópia értékeit az anyagok standard állapotára adják meg. A 32. táblázatban a standard képzödési entalpia és az abszolút entrópia értékek találhatók különbözö anyagokra. A standard képzödési entalpia () egységében kJ, az abszolút entrópia (S^o) egységében pedig J szerepel, ezért a táblázatban a értékek mértékegysége 1000-szer nagyobb az S^o-mértékegységénél. A táblázat S^o adataiból látható, hogy a gázok entrópiája nagyobb, mint a folyadékoké. A tiszta, szilárd anyagok entrópiája a legkisebb. Az entrópia a bonyolultabb molekulaszerkezettel is növekszik, amire példa a naszcensz oxigén, az oxigénmolekula és az ózon; a víz és a hidrogén-peroxid; valamint a vas, a Fe₂O₃ és a Fe₃O₄ abszolút entrópia értékei. Mindezek összhangban vannak az abszolút entrópia additivitásával.

29. táblázat. Standard képzödési entalpia és abszolút entrópia értékek

A kémiai reakciókat kísérö entrópia változás

A kémiai reakciókban az entrópia változik, mert változik a molekulák és az ionok száma, mert halmazállapot-változás következik be, és mert változik a részecske geometriája és bonyolultsága. Ezek alapján a folyamatot kísérö entrópia változásokat, legalábbis kvalitatíve, könnyü megjósolni, de az abszolút entrópiák ismeretében a DS^o számolására is van lehetöség. A dinitrogén-oxid bomlása során (2 N₂O (g) = 2 N₂ (g) + O₂ (g)) gázfázisú reakcióban kettö mól nitrogénoxid gázból három mól nitrogén és oxigéngáz keletkezik, ezért nagy entrópia növekedésre számíthatunk. Az abszolút entrópia értékekböl T = 298 K-on DS^o a következöképpen számítható:

DS^o = (2ˇ191,6 J/K + 205,1 J/K) - 2ˇ219,9 J/K = 148,5 J/K.

Azaz ebben a reakcióban az entrópia növekedés 148,5 J/K.

A szén oxidációja során (2 C(s) + O₂(g) 2 CO(g)) a molekulaszám ugyan csökken, de a gázállapotú anyag mennyisége nö, ezért jelentös entrópia növekedés várható:

DS^o = 2ˇ197,9 J/K - (2ˇ5,7 J/K + 205,1 J/K) = 179,3 J/K.

Az abszolút entrópia értékekböl számolva az entrópia növekedést 179,3 J/K.

A sósav képzödési reakciója (H₂(g) + Cl₂(g) 2 HCl(g)) gázfázisban megy végbe; nem változik a molekulák száma, ezért kicsiny az entrópia változás:

DS^o = 2ˇ 186,9 J/K - (130,7 J/K + 223,1 J/K) = 20,0 J/K.

Ebben az esetben az entrópia változás 10-15%-a az elöbbi két folyamaténak.

Az ammóniaszintézis során (N₂(g) + 3 H₂(g) 2 NH₃(g)) 4 mól kiindulási anyagból 2 mól termék keletkezik, ezért nagy entrópia csökkenés várható:

DS^o = 2ˇ 192,4 J/K - (191,6 J/K + 3ˇ130,7 J/K ) = -198,9 J/K.

Az entrópia csökkenés mértéke az ammóniaszintézis esetében -198,9 J/K.

Szabadentalpia és szabadenergia

A természetben önként végbemenö folyamatok a termodinamika I. fötétele szerint az entalpiacsökkenés, a termodinamika II. fötétele szerint pedig az entrópia növekedés irányába mennek végbe. Gibbs 1876-ban a spontán jelleg két kritériumát egyesítette; szerinte egy önként lejátszódó folyamat entalpia- (vagy belsöenergia) csökkenése két részböl tevödik össze:

* az egyik rész szabadon átalakítható az energia más fajtájává, vagyis a rendszer munkavégzö képességét jelenti,

*a másik rész ahhoz szükséges, hogy adott hömérsékleten tartva a rendszert biztosítsa annak rendezettségét (rendezetlenségét), ezért munkává nem alakítható át.

Fentiek szerint tehát,

entalpia = szabadentalpia + át nem alakítható energia,

azaz

H = G + Tˇ S ,

ahol G = szabadentalpia, amely a rendszer maximális munkavégzö képességét jelenti az egyensúlyi állapot eléréséig,

a Tˇ S szorzat pedig a munkává át nem alakítható energiát jelöli.

Ennek értéke T= 0 K-on nullává válna, amiböl az következik, hogy csak abszolút nulla hömérsékleten lenne az entalpia teljesen átalakítható hasznos munkává (H=G).

A szabadentalpia-változást szintén a kezdeti és a végállapot határozza meg, melynek értéke állandó nyomás esetén:

DG = DH - Tˇ DS.

Fenti egyenlet segítségével megjósolható a folyamatok spontán lejátszódása:

*ha DG < 0 a folyamat exergonikus és önként végbemegy,

*ha DG > 0 a folyamat endergonikus és önként nem játszódik le,

*a DG = 0 a rendszer termodinamikai egyensúlyi állapotban van.

A Gibbs-féle szabadentalpia-változás meghatározza a kémiai folyamatok irányát. Az önként végbemenö reakciók szabadentalpia-csökkenéssel járnak, melynek során a rendszer egyensúlyba kerül környezetével amikor DG = 0, azaz a DG által biztosított hasznos munkavégzés lehetösége megszünik. Állandó térfogaton lejátszódó reakciókban az entalpiaváltozás helyett a belsöenergia-változással kell számolni, mivel itt nincs térfogati munka. Az ilyen folyamatok hasznos munkavégzését a szabadenergia-változás (DF) adja meg:

DF = DE - TˇDS.

A szabadenergiát és a szabadentalpiát termodinamikai potenciálfüggvényeknek is nevezzük, mivel hasonló szerepet töltenek be a termodinamikában, mint a potenciális energia fogalma a mechanikában.

Mind a szabadentalpia, mind a szabedenergia állapotfüggvény és extenzív sajátság; mértékegységük a joule (J). Mindkettö definiálására használt egyenletben ugyanaz a tag, a TˇS szerepel. Ennek izoterm körülmények közötti megváltozása a TˇDS, amely az entalpia vagy az energia munkává át nem alakítható részét, az ún. kötött energiát jelöli. Tehát a DG és a DF az entalpia ill. belsö energia munkavégzésre felhasználható része, ezért a szabadentalpia ill. szabadenergia változást az önként végbemenö folyamatok hajtóerejének tekintjük, amely a folyamat elörehaladtával a nullához tart.

Megfelelö körülmények között azonban olyan termodinamikai folyamatok is végbemehetnek, amelyek önmagukban véve szabadentalpia növekedéssel járnak. Ezek a folyamatok úgy játszódnak le, hogy végbemenetelüket egy nagymértékü szabadentalpia-csökkenéssel járó folyamat elösegíti. Egy DG₁ > 0 szabadentalpia-változással járó reakció pl. végbemehet, ha hozzá egy DG₂ < 0 szabadentalpia-változással járó reakció kapcsolódik, és DG₂ > DG₁. Ekkor ugyanis

DG₁ + DG₂ <

Az ún. kapcsolt reakciókra számos példát szolgáltat a biokémia, melyröl a késöbbiekben még lesz szó.

A szabadenergia- és szabadentalpia-változások hömérséklet függöek. Külön figyelemre méltó a

TˇDS tag,

melynek jelentösége annál nagyobb, minél magasabb hömérsékleten játszódik le a folyamat. A hömérséklet hatása oly mértékü lehet, hogy a DG vagy DF negatívvá válhat, és így a folyamat önként lejátszódása szempontjából sem közömbös. A 30. táblázat a hömérséklet befolyását mutatja a kémiai reakciók lejátszódására.

30. táblázat. A hömérséklet hatása a kémiai reakciók lejátszódására

A táblázatból látható, hogy az exoterm reakciók nem játszódnak mindig le spontán, azaz nem szükségszerüen exergonikusak. Endoterm reakciók is végbemehetnek önként, ha a reakció során az entrópia növekszik, és a hömérséklet is megfelelöen magas.

Standard szabadentalpia

A szabadentalpia értéke függ a rendszer tömegétöl és hömérsékletétöl, a gázok esetében még a nyomástól, az oldatok esetében pedig még a koncentrációtól is. Az összevethetöség és a változások kiszámíthatósága céljából vezették be a standard-szabadentalpia (G^o) fogalmát, amely alatt 1 mól anyag szabadentalpia-tartalmát értjük 0.1 MPa nyomáson és 298 K hömérsékleten. Mértékegysége a J/mol. Oldatok esetében a definícióba még az is beletartozik, hogy a reakciópartnerek koncentrációja egységnyi, azaz 1 mol/dm³. Biológiai rendszerek esetében még azt is kikötjük, hogy a pH-értéke 7. Ez utóbbi esetében a szabadentalpia jelölése: G^o'.

Megállapodás szerint a kémiai elemek standard belsöenergiája (U^o), standard entalpiája (H^o) és standard szabadentalpiája (G^o) is nulla. Ez arra a halmazállapotra ill. módosulatra vonatkozik, amely standard körülmények között a legstabilabb.

A standard állapotú kiindulási anyagokat és termékeket feltételezve a Gibbs-féle egyenletböl következtethetünk a kémiai reakciók lejátszódásának alapvetö feltételeire.

DG^o = DH^o - TˇDS^o.

Ha DH^o és DS^o elöjele ellentétes, akkor a folyamat iránya:

*önként lejátszódik (DH^o < 0 és DS^o > 0),

*önként soha nem megy végbe (DH^o > 0 és DS^o < 0).

A többi esetben a hömérséklet lényegesen módosítja a spontán lejátszódást.

A standard szabadentalpia-változás és a kémiai egyensúly

Egy egyensúlyra vezetö kémiai reakciókban

A + B C + D ,

a szabadentalpia-változás adott idöpillanatban:

DG = DG^o + RTˇ ln ,

ahol a koncentrációk a kiindulási anyagok és a termékek egy t idöpontban mért nem egyensúlyi (ne) koncentrációit jelölik.

A DG^o az A, B, C és D anyag standard szabadentalpia értékeiböl számítható 1 mól koncentráció esetén. A reakció elörehaladtával kialakul az egyensúlyi állapot, amikor a DG = 0, és amikor az egyenletben szereplö koncentrációk az egyensúlyi koncentrációkat jelölik:

0 = DG^o + RTˇ ln .

Mivel az utóbbi egyenletben szereplö tört definíciószerüen a kémiai egyensúlyi állandót jelenti, vagyis:

K = .

Az egyenletbe behelyettesítve az egyensúlyi állandót, némi átrendezés után az alábbi egyenlöség írható fel:

DG^o = -RTˇ ln K.

Áttérve a 10-es alapú logaritmusra az alábbi összefüggést kapjuk:

DG^o = -2,303ˇ RTˇ log K.

Ha az egyensúlyi állandót ismerjük, ezen összefüggés alapján tájékozódhatunk arról, hogy a kémiai folyamat önként végbemehet vagy sem. Önként lejátszódó folyamatokban DG^o<0, ezért K>1, azaz standardállapotú anyagokból kiindulva a termékek koncentrációja egyensúlyban nagyobb, mint a kiindulási anyagoké. Ha viszont K<1, DG^o>0, tehát valószínü, hogy a reakció önként nem megy végbe. Természetesen így általában csak becslésre van lehetöségünk, mivel többnyire nem standard állapotban lezajló történésekkel foglalkozunk. A 15. táblázat adatai a biokémiai folyamatoknál szokásos pH = 7 értéken mért szabadentalpia változást (a DG^o'-t) hasonlítja össze az egyensúlyi állandóval.

A biokémiai reakciókra vonatkozó standard szabadentalpia-változás egységnyi vízkoncentrációra és semleges pH-ra vonatkozik.

A kémiai reakció lejátszódásának tényleges hajtóereje a DG, a különbözö folyamatok összehasonlítására pedig a DG^o használható. Egy adott reakcióban a DG viszonyát a DG^o-hoz a kezdeti koncentrációk aránya szabja meg, a folyamat tényleges irányát viszont a DG határozza meg.

31. táblázat A DG^o' és K összefüggése 25 ^oC-on

Szabadentalpia-változás néhány biokémiai reakcióban

A kémiai reakciók a sejtekben nem elszigetelten játszódnak le, hanem párhuzamosan, sorozatreakciókban ill. körfolyamatokban. Így válik érthetövé az, hogy szabadentalpia- növekedéssel járó (tehát termodinamikailag kedvezötlen) reakciók is végbemennek akkor, amikor szabadentalpia-csökkenéssel járó reakcióval kapcsolódnak össze. Ezt lehet szemléltetni az L-malát átalakulásán L-aszpartáttá:

L-malát fumarát + H₂O K₁ = 0,21 = +3,72 kJ/mol.

Ez a reakció a fumaráton keresztül az erösen exergonikus

+ fumarát L-aszpartát K₂ = 528 = -15,40 kJ/mol,

reakcióhoz kapcsolódik, és így végsö soron egy szabadentalpia csökkenéssel járó összetett folyamat valósul meg. Ebben a reakciósorban az elsö lépés endergonikus, ezért az L-malát koncentrációja közel 5-szöröse a fumaráténak; a második reakció exergonikus, ez a lépés teljesen lejátszódik. A két részfolyamat együttesen szabadentalpia-csökkenést hoz létre:

DG^o' = + = -11,68 kJ/mol <

Ha az ennek megfelelö egyensúlyi állandót K-val jelöljük, a legutóbbi egyenlöség helyett az alábbi is felírható:

-RT lnK = -RT lnK₁ - RT lnK₂, amiböl

K = K₁ˇ K₂ = 111

Tehát az egyensúly az L-aszparát képzödés irányába tolódik el.

A tápanyagmolekulák szabadentalpia tartalmának felhasználásában és a szabadentalpia-növekedéssel járó makromolekulák szintézisében központi szerepet töltenek be a foszfáttartalmú köztitermékek. A foszfátcsoport átvitelét kísérö szabadentalpia-változások összehasonlítására ezen intermedierek hidrolízisenergiáit használjuk fel. A foszfátcsoport hidrolízise során a pH-tól függöen foszforsav ill. a foszforsav anionjai keletkeznek.

A 32. táblázat néhány intermedier hidrolízis energiáit mutatja.

32. táblázat. Foszfáttartalmú intermedierek hidrolízis energiája

25 ^oC-on, pH= 7,0 esetén

(ATP, ADP, AMP: adenozin-tri-, di- és monofoszfát). A 35. táblázatból látható, hogy sok vegyület hidrolízise nagy szabadentalpia-csökkenéssel jár, másoké viszont csak csekély mértékü. A foszfoenol-piruvát hidrolíziséhez kapcsolódhat szabadentalpia-növekedésével járó folyamat, mint amilyen pl. az ATP szintézise.

Foszfoenol-piruvát + H₂O = Piruvát + P_i DG^o' = -61,9 kJ/mol

ADP + P_i = ATP + H₂O DG^o' = + 40,2 kJ/mol

A reakcióban P_i -vel jelöltük a foszfátion különbözö formáit pH = 7,0-en.

Az ATP-szintézishez szükséges energia megegyezik a hidrolízisenergiával, csak azzal ellentétes elöjelü. A két reakció együttes mérlege:

Foszfoenol-piruvát + ADP = Piruvát + ATP DG^o' = -21,7 kJ/mol,

amely spontán lejátszódó folyamatot mutat.

A hidrolízis-reakciók nagy szabadentalpia-csökkenése (DG^o' < -30 kJ/mol) az intermedier és a foszfátion szerkezetével magyarázható. A tetraéderes hibridállapotú foszfátion 4 kovalens s-kötést alkot 4 oxigénatommal a foszfátionban, míg az ötödik kovalens p-kötés 1-1 oxigénatomhoz lokalizálódik. A kialakuló négy határszerkezet rezonanciája delokalizálja a p-kötést (1 s és 1/4 p-kötést hozva létre a foszfor és oxigénatomok között), alacsonyabb energiaállapotot kialakítva. Az intermedierekben található foszfátcsoport (ATP-ben savanhidrid kötésben) rezonanciája nem, vagy csak részben érvényesül, ezért energiatartalma magasabb. Vízzel való reakciója során szabadul fel ez az energia, amikor a foszfátion rezonanciája teljessé válik.