Bevezetö ismeretek a MATLAB modellezö és szimulációs program használatához

A MATLAB (Matrix Laboratory) a MATH WORKS Inc. által kidolgozott és folyamatosan fejlesztett, bövített szoftver. A MATLAB Microsoft a Windows programra támaszkodik. A szabályozástechnikai feladatok szimulációs vizsgálatához és a megoldások, a megvalósítások tervezéséhez, ellenörzéséhez nyújt igen széleskörü segítséget. A teljes szoftver több részegységböl épül fel (pld. jelfeldolgozás, szabályozás, optimalizálás, neurális hálózatok stb.), és ezek önmagukban egy-egy adott témát fognak át. A MATLAB részletes megismeréséhez a szoftver csomagokkal együtt kézhez kapott User's Guide (Használói útmutató) szolgál. A következö részben a MATLAB szabályozástechnikai vonatkozásainak néhány alapvetö ismeretét foglaljuk össze és nem térünk ki a késöbbiekben tárgyalt anyagrészekben nem alkalmazott részletekre..

A állandóan fejlesztett MALAB szoftverek kis mértékben eltérnek egymástól és újabb-újabb részletekkel gazdagodnak. Ebböl eredöen lehet, hogy a következö részekben ismertetett eljárások a felhasználó által birtokolt szoftverben ‑ csak kis mértékben ‑ módosítva használhatók. A példák a MATLAB VERSION 5.2.0.3084 jelü programmal készültek.

Elemi számítások

A MATLAB program behívása után a képernyön a Co 959b15j mmand Widow fejrész jelenik meg. A különbözö információkat tartalmazó sorok alatt, a képernyö bal szélén >> jel látható. Egy új programsor beírása mindig ezen jel után történhet. A sorok zárása és a programba illesztése az ENTER billentyü leütésével valósul meg. A további részekben (amennyiben ennek ott kiemelt szerepe is van) ╝ jelzéssel hívjuk fel a figyelmet az ENTER alkalmazására ( feltüntetése késöbbi példákban elmaradhat). A MATLAB csak tizedes pontot ismer fel. Egy-egy alapvetö és általános utasításra ► jelzésü sor emlékeztet.

►az elemi számítások elvégzéséhez a + , a ‑ , a * , a / utasításokat kell alkalmazni.

Példa: 16/4 ╝

ans=

4

►a hatványozás ^jellel történik

Példa: 3.33^2 ╝

ans=

11.0889

Kezdö gyakorlatként alakítsunk ki egy 3x3 méretü mátrixot.

(A sorkezdö >> jelet a továbbiakban nem tüntetjük fel.)

A = [1 2 3;4 5 6;7,8 10]     ╝ (1)

A mátrix kiírásra kerül:

A =

1 2 3

4 5 6

7 8 10 alakban.

► Amennyiben a programsor végére, itt most az (1) példasor ] zárójele után ; (pontosvesszö) kerülne, úgy a sor, - itt a mátrix elemei - kiírás nélkül kerül elmentésre.

► a programsort magyarázó szövegrészek % jel mögött következnek

A következö részekben - példák segítségével - a MATLAB elsösorban szabályozástechnikai problémák megoldásánál történö alkalmazását mutatjuk be.

_{Jelleg görbéket leíró egyenletek állandóinak meghatározása}

_{a = [0 4 6 8 10 12 14 16 18 20]; % a vizsgált átviteli tag bemenö jelei}

_{b = [4 12 16 20 24 28 32 36 40 44];                             % a vizsgált átviteli tag kimenö jelei (lineáris)}

_{plot (a,b);grid}            

_{a plot utasítás az a és b adatokhoz tartozó görbét egy koordináta rendszerben kirajzolja,}

_{a grid utasítás a koordináta rendszeren belül egy hálózatot is berajzol.}

_{polyfit [ a, b, 1 ] % a polyfit utasítás a közelítö egyenlet állandóit elsö rendü közelítéssel, - erre utal az 1 érték - számítja ki}

_Válasz:

_{ans =}

_{2.0000 4.0000 2.00.. a meredekség,}

_{a tengely metszet}

_{A meredekség itt ( lineáris tagot vizsgálunk ) az átviteli tényezö értéke is}

_{c = [ 0 0.45 0.61 0.71 0.79 0.87 0.94 1.00 1.06 1.12 ];}                

_{% a vizsgált (nem lineáris) átviteli tag kimenö jelei}

_{plot (a,c);grid % az a és c adatokhoz tartozó görbét hálózattal rajzolja ki}

_{polyfit [ a, c, 2 ] % a közelítö egyenlet állandóit másod rendü közelítéssel számítja ki,}

_Válasz:

_{ans =}

_{-0.0024 0.1000 0.0464 -0.0024... a másodrendü tag együtthatója}

_{az elsörendü tag együtthatója}

_{tengely metszet}

_Ellenörzés

_{f = (-0.0024*(12^2)) + 0.1*12 + 0.0464 % egy másodrendü függvénynek f nevet adva és az értékeket behelyettesítve}

_Válasz:

_{f =}

_{a c. adatsorban az a=12-höz tartozó kimenöjel 0.87 értékü, de az eltérés elfogadható}

_{jobb egyezés érdekében esetleg magasabb rendü közelítéssel újra lehet számolni}

_{A két adatsor párhoz tartozó diagram:}

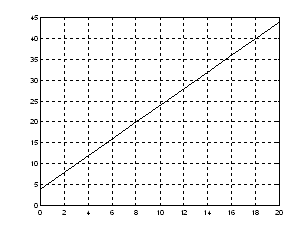
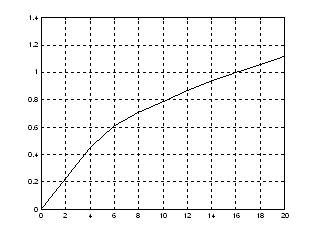
A következö példákban lineáris átviteli tagok bemenö/kimenö adatai vannak. Számítsa ki MATLAB segítségével a leíró egyenlet együtthatóit, az átviteli tényezöt és a tengelymetszet értékeket. Ábrázolja a jelleggörbét.

(A=0.33)

(A=1.28)

3.

(A=5.56)

A következö példákban nem lineáris átviteli tagok bemenö/kimenö adatai vannak. Állapítsa meg a k és a c értékét, számítsa ki az átviteli tényezöt például a bemenö=4 munkapontban. Ábrázolja a jelleggörbét és grafikusan is ellenörizze a munkaponti átviteli tényezöt.

y = c . x²  + k alakú

y = c + k alakú

y = c . x³  + k alakú

_{Több átviteli tagból álló elemcsoport eredö átviteli függvénye}

Az átviteli függvények ismeretében eredö átviteli függvények kiszámíthatók. A MATLAB csak két átviteli függvény eredöjét tudja kiszámolni, több tag esetén fokozatosan, párokat alakítva ki lehet eredöt számítani.

parallel két párhuzamosan kapcsolt átviteli függvény eredöje

series               két sorba kapcsolt átviteli függvény eredöje

feedback negatív visszacsatolású rendszer eredö átviteli függvénye

Példa: negatív visszacsatolásra

nu1=5;                         % elörevezetö ág átviteli függvény számlálója

de1=[5 1]; % elörevezetö ág átviteli függvény nevezöje

nu2=1;                         % visszacsatoló ág átviteli függvény számlálója

de2=[1];                      % visszacsatoló ág átviteli függvény nevezöje

sys1=tf(nu1,de1) % elörevezetö ág átviteli függvény kiszámítása

Eredmény: Transfer function:

5

5 s + 1

» sys2=tf(nu2,de2)       % visszacsatoló ág átviteli függvény kiszámítása

Eredmény: Transfer function:

sys=feedback(sys1,sys2) % negatív visszacsatolt rendszer átviteli függvény kiszámítása

Eredmény:      Transfer function:

5

5 s + 6

Az eredö átviteli függvény tehát:    5 / (5 s + 6)

a szokásos formátum eléréséhez (azaz arányos tag esetében a nevezö utolsó tagja 1 legyen) 6-tal osztva:

0.83 / (0.83 s+ 1)

Példa: két párhuzamosan kapcsolt tag eredö átviteli függvénye

nu1=[5];                                  % a két átviteli tag átviteli függvényeinek számlálója/nevezöje

de1=[3 1];

nu2=[3];

de2=[5 1];

sys1=tf(nu1,de1);                    % a két átviteli függvény

sys2=tf(nu2,de2);

parallel(sys1,sys2)

Eredmény:

Transfer function:

34 s + 8

15 s^2 + 8 s + 1

A függvény vizsgálatával megállapítható, hogy ez a két párhuzamosan kapcsolt, nem azonos nevezöjü átviteli tag eredöje 2 idöállandóval jellemezhetö differenciáló tagot eredményez. Utóbbi megállapítás a számlálóban lévö 8 kiemelésével jól látható: 8*( 4.25.s + 1) (Emlékeztetö: az átviteli függvény számlálójában lévö (Laplace) s-jel differenciáló tulajdonságra utal).

Átmeneti függvény kialakítása és tanulmányozása

Az átmeneti függvény az átviteli tag ugrásjelre adott (idöben lefutó) válaszfüggvénye

Az átviteli függvény ismeretében az átmeneti függvény megszerkesztö. A MATLAB programozásnál az átviteli függvény számlálóját és a nevezöjét külön-külön kell rögzíteni - és ha szükséges - számindexxel megkülönböztetni

◄ az átviteli függvény számlálóját célszerü nu ( numerator) a nevezöjét de (denumerator) betüjelekkel rövidíteni - és ha szükséges - szám indexszel (pl. de2) ellátni.

Egyes MATLAB verziók megkövetelik a nu.., és de. értékekböl kialakított sys...rendszert., de vannak verziók, amelyek a nu. és de.bevitelt is elfogadják. A sys a rendszer átviteli függvénye és

sys= tf(nu.,de.)

utasítással alakítható ki.

◄ az átmeneti függvény a step(sys..)  utasításra rajzolódik ki.

_{Példák átmeneti függvények megismerésére}

_{Két P1T tag átmeneti függvényének kirajzolása egy diagramon, majd a két P1T tag összeszorzása és a kialakult P2T tag átmeneti függvényének rárajzolása az elözö diagramra.}

nu1=[5];                      % 1 indexü P1T tag

de1=[2 1];

sys1= tf(nu1,de1); % kialakítja az elsö P1T tag átviteli függvényét

step(sys1);grid             % kirajzolja az elsö átmenetit-

hold on                        % rögzíti az átmeneti görbés diagramot

nu2=[3];                                  % 2 indexü P1T tag

de2=[0.5 1];

sys2=tf(nu2,de2); % kialakítja a másik P1T tag átmenetit

step(sys2);grid             % kirajzolja a második átmenetit

hold on                        % rögzíti az átmenetit

P2T tag kialakítása:

[sys3]=series(nu1,de1,nu2,de2) % a két P1T szorzata ki is írva

_Válasz:

num =

0 0 15

dem =

1.0000 2.5000 1.0000 % P2T tag. átv. fgv.:

15 / (1 s² + 2.5 s + 1)

step(sys3);grid % kirajzolja a két tag szorzatának átmenetijét

megfigyelendö

állandósult értékhez közeledés;

a két átviteli függvény összeszorzásának eredménye

idöállandó értelmezése

a P1T és P2T görbék alakjának origó közeli különbsége

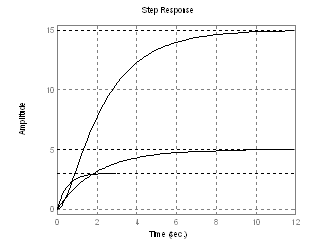
P3T tag átmeneti függvényének tanulmányozása

% (az elözö diagramot törölni)

nu4=[2];

de4=[64 16 8 1];                     % P3T tag, átlagos T = 4

sys4=tf(nu4,de4)

step(sys4);grid             % ez látható a következö diagramon

megfigyelendö

látszólagos holtidö

lengés hajlam; ennek tanulmányozására de4= 8 értékét csökkentse 4-re, majd növelje 16-ra (azaz változtassa a csillapítási tényezöt)

rajzoltassa ki a görbéket és figyelje meg a lengés hajlam változását (csillapítási tényezö változásának hatása)

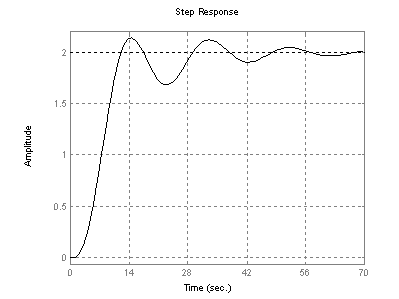
Példák összetett átviteli rendszerek átmeneti függvényeinek vizsgálatára.

1. Csövezeték és a hozzá kapcsolt tartály dinamikus tulajdonsága

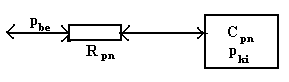
A csövezeték pneumatikus ellenállásként ( R_pn ), a tartály pneumatikus kapacitásként( C_pn) viselkedik. Ugyanis a különbözö fojtások - ilyenek a csövek, szelepek, stb. - ellenállását az elemeken jelentkezö nyomásesés és közegáram hányadosaként definiálhatjuk. ( analógia: a villamos feszültség és a villamos áram hányadosa az ellenállás ). Hasonló analógia van a villamos kapacitással. A falakkal elhatárolt térben bezárt gáz tömegének megváltozása nyomásváltozást okoz. A változás mértéke a tér pneumatikus kapacitásától függ.

A pneumatikus ellenállás illetve kapacitás tehát:

R_pn = dp / q_m

dp/dt = (1/C_pn ) *(dm/dt);

C_pn = q_m / (dp/dt)

R_pn   [ 1 / m.s ]; C_pn [ m.s² ];

ahol: dp/dt a nyomás változása, Pa/s;

dm/dt : a tömegáram: q_m, kg/s.

A csövezeték + tartály - a villamos RC taghoz hasonlóan ‑ pneumatikus RC tagnak tekinthetö és az idöbeni viselkedését a következö differenciál-egyenlet írja le:

ahol: T= R_pn .C_pn a rendszer idöállandója;

( ellenörizze: az R_pn .C_pn  szorzat valóban idö dimenziót eredményez ? )

p_k a rendszer idöben változó (kimenö) nyomása

p_b a rendszer (ugrásjel formában megváltoztatott) bemenö nyomása.

A differenciál-egyenlet Laplace transzformációjával kapott összefüggés és az ebböl származtatott átviteli függvény:

A rendszer átmeneti függvénye a MATLAB segítségével a következö utasításokkal jeleníthetö meg:

nu=[1];

de=[12 1];                               % T = 12 választással

sys=tf(nu,de);

step(sys);grid

A diagramon látható kimenö jelváltozás egységnyi ugrásjelre adott idöadat. Az átviteli függvény számlálója=1, tehát a változás az egységnyi ugrásjel értékéhez tart. Amennyiben a számláló más értékü, úgy az állandósult állapot ezen értéket éri el.

2. Pneumatikus RCR tag vizsgálatra

Mind az (ipari) gázvezetékek, mind a pneumatikus automatikai eszközök egymáshoz illeszkedö fojtások (pneumatikus ellenállások) és pneumatikus kapacitások kapcsolatából alakulnak ki. Az ábra egy ilyen rendszer blokkvázlatát mutatja be.

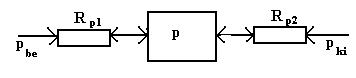
A pneumatikus RCR tag átviteli tulajdonságának ismerete a rendszer alkalmazásánál elengedhetetlen, hiszen viselkedése a (jel)terjedést módosítja, elösegíti vagy csillapítja. A választott kimenö jellemzö a kapacitásban uralkodó p nyomás és ennek megfelelöen a leíró differenciál-egyenlet:

A differenciál-egyenlet bal oldala a kapacitásban kialakuló nyomást írja le, és hasonló az elözö példa differenciál egyenletéhez. A jobb oldalon a rendszerre ható bemenö nyomás és a kapacitás után következö (csö)szakasz ellenállása, mint a kapacitásban kialakuló nyomást ugyancsak befolyásoló - az ellenállások viszonyától és a p_k  értékétöl függö, egy adott körülmény között állandó értékü ‑ tag szerepel. Amennyiben p_k = 0, a jobb oldalon csak az elsö tagnak van szerepe. Növelt p_k a p értékét csökkenti. Ha R_p2-t lezárjuk és így ennek ellenállása végtelen, az 1. példa egyenletéhez jutunk.

Az R_p1 / ( R_p1 + R_p2 ) és a másik hasonló alakú tört a pneumatikus nyomásosztás alapösszefüggése. (Az analógia az elektromos feszültségosztóval ismét felismerhetö!)

Az RCR tag vizsgálatára a következö értékeket választjuk:

p_b = 500 Pa; p_k = 300 Pa; R_p1 =2 ( 1/m.s ) R_p2 = 8 ( 1/m.s) C=3 ( m.s² )

Ennek megfelelöen a két tört értéke: 0.8 illetve 0.2.

A differenciál-egyenlet a behelyettesítés után:

A differenciál-egyenlet vizsgálatával megállapítható, hogy egy két-bemenetes rendszert kell modellezni. Az egyik bemenet a p_b bemeneti nyomás, míg a másik bemenet a rendszer kimeneti p_k kimeneti nyomása. A Laplace transzformálás után az átviteli függvény kialakítható.

Az átviteli tényezö a differenciál-egyenlet jobb oldalának kiszámolt értéke itt a példában: 460 Pa. A T értéke pedig: 4.8 szekundum.

A MATLAB szimuláció:

nu=[460];

de=[4.8 1];

sys=tf(nu,de)

step(sys);grid

( Gyakorlásként változtassa meg az ellenállások és a nyomások érétkeit és tanulmányozza a görbék alakját és az állandósult értékek változásait. )

A megismert pneumatikus RCR tag viselkedésének vizsgálatára a MATLAB/SIMULINK szimulációs szoftver is alkalmazható.

3. Folyadéktágulás elvén müködö csörúgós hömérö viselkedésének vizsgálata.

A müszer a mérendö térbe nyúló vastagabb, folyadékkal feltöltött csöböl és az ehhez csatlakozó, a hö okozta térfogatváltozást a rúgós kijelzö részhez elvezetö kapilláris csöböl áll. A hö okozta térfogatváltozás egy mutató elmozdulását eredményezi.

A következö részben használt jelölések:

J_k környezeti hömérséklet K;

dx elemi magasság az érzékelö felületen m;

t idö h;

J_m az érzékelö hömérséklete K;

d az érzékelö átméröje m;

c a folyadék fajhöje kJ/kg.K;

ρ a folyadék sürüsége kg/m³ ;

α felület höátadási tényezö kJ/m² .K. s

A hö-mérleg egyenletek kialakítása:

A belépö höáram:

J_k J_m α.d.dx.π ;               (a 3 utolsó tag adja a felületet)

Az idöegység alatt felvett hömennyiség:

(dJ_m dt ). c (d² π/4) . dx . ρ;               ( a 3 utolsó tag a tömeg)

A hö-áram és a felvett hömennyiség azonos, tehát a két összefüggés egyenlö. Az egyszerüsítések és átrendezés után:

Az állandókat tartalmazó tört idö dimenziójú és így a müszer T idöállandójának tekinthetö. Ezzel a helyettesítéssel a differenciál-egyenlet egy, egyetlen idöállandóval jellemezhetö átviteli tag (P1T) dinamikus viselkedését tükrözi vissza.

(Megjegyzés: ez a modell az érzékelö rész fémböl készült falának viselkedését és tulajdonságait figyelmen kívül hagyja; amennyiben a modellbe ezeket is beillesztjük, legalább két energiatárolót kell figyelembe venni, és így már PNT tag alakul ki.)

Az átmeneti függvény vizsgálatához a következö értékeket vegyük figyelembe:

c 2.2 kJ/ kg.K

d 0.005 m

ρ 900 kg/m³ ( a folyadék alkohol )

α 3.4 kJ/m².s.K

A hömérö idöállandója tehát T=3.1 szekundum.

Az átviteli függvény:

számlálója: 1 ( az átmeneti állapot végén a hömérö a külsö hömérséklettel azonos állapotba kerül, tehát a jel nem gyengül és nem erösödik, azaz az átviteli tényezö: 1 );

nevezöje: ( 3.1 s + 1 ).

A MATLAB futtatás bemenö változói tehát nu=[1]; illetve de=[3.1 1];

A már ismert módón alakítsa ki a sys-függvényt, step utasítással rajzoltassa ki az átmeneti függvényt.

► hold utasítással rögzítse a függvényt,

majd változtassa a nevezöben lévö idöállandó értékékeket ( pl. de1=[4.5 1], stb.) és mindig alakítson ki az új nevezöknek megfelelö újabb sys függvényeket ( pl: sys1=tf(nu,de1), step utasítással rajzoltassa rá az elözö diagrammra az új függvény görbéjét. Figyelje meg a különbözö idöállandó értékek hatását a görbék lefutásán.

Integráló tagok átmeneti függvényének megismerése

Idökésés nélküli tag

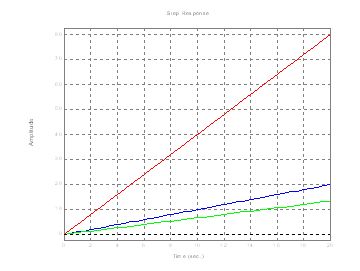
Az átviteli függvény Y(s)= 1 / 1.s (egyszerü integráló tag amelynek az erösítése:1)

nu1=[1]; % az integráló tag átviteli függvényének számlálója

de1=[1 0]; % az integráló tag átviteli függvényének nevezöje

a zárójelen belüli utolsó tag: 0 (és nem 1, mint a P tagoknál)

sys1= tf(nu1,de1); % az átviteli függvény kialakítása,; nincs kiírva a jel beírása miatt

step(sys1,20);grid % kirajzolja az átmenetit ( 20 idöegységre )

hold on

nu2=[4];                      % az átviteli tényezöjü tag számlálója: 4

sys2= tf(nu2,de1);

step(sys2,20);grid % kirajzolja az átmenetit

hold on

de2=[6 0];                   % az átviteli tag nevezöje: 6, az erösítés tehát: 4/6

sys3=tf(nu2,de2);

step(sys3,20);grid % kirajzolja az átmenetit

megfigyelendö

az eltérö irány-tangesek oka és hatása (a számláló(nu) és a nevezö(de) elsö tagjának hányadosa határozza meg a meredekséget)

Idökéséses integráló tag

Miután kitörölte az elözö diagramot, építse fel az idökéséses integráló tagot. Az átviteli függvény nevezöje maradjon nu2=4, és csak a nevezöket változtassuk.

de1=[3 1 0];

sys4= tf(nu2,de1];

step(sys4,20);grid % kirajzolja az átmenetit 20 sec. idöben

hold on

de2=[2 1 0];                            % rövidebb idöállandóval

sys5= tf(nu2,de2);

de3=[1 1 0];                            % még kisebb idöállandóval

sys6= tf(nu2,de3);

step(sys5,20);grid

hold on

step(sys6,20);grid

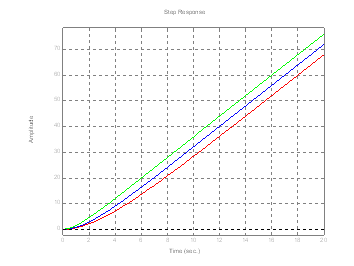
megfigyelni

az irány-tangesek hasonlóak,

az indulásnál látszólagos holtidö

az egyes görbék egy-egy szekundummal vannak eltolódva

Differenciáló tagok átmeneti függvényének megismerése

Idökésés nélküli tag (megjegyzés: ezt a függvényét a MATLAB nem tudja megoldani)

Differenciáló tag egy idöállandóval

nu1=[3 0];                               % a tag átviteli függvényének számlálója

a zárójelen belüli utolsó tag: 0 ;(ez jellemzö a D-tagra)

de1=[3 1];                               % a tag átviteli függvényének nevezöje

sys1=tf(nu1,de1);                     % kiszámítja az átviteli függvényt, de nem írja ki

step(sys1);grid             % az átviteli tényezö=3

hold on

nu2=[1.5 0];

sys2=tf(nu2,de1);

step(sys2);grid             % az átviteli tényezö=1.5

hold on

de2=[5 1];                               % az idöállandó 3 helyett itt 5

sys3=tf(nu2,de2);

step(sys3);grid            

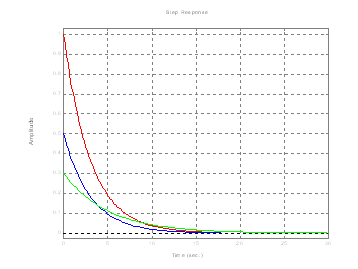
megfigyelnii:

a nagyobb átviteli tényezö ( nu ) nagyobb csúcsot okoz

a nagyobb idöállandó lassítja a lecsengést és csökkenti a csúcsot is

Példatár anyaga:

Bevezetö ismeretek a MATLAB modellezö és szimulációs program használatához

Elemi számítások

_{Jelleg görbéket leíró egyenletek állandóinak meghatározása}

_{Több átviteli tagból álló elemcsoport eredö átviteli függvénye}

_{Átmeneti függvény kialakítása és tanulmányozása}

Példák összetett átviteli rendszerek átmeneti függvényeinek vizsgálatára.

Pneumatikus RC tag

Pneumatikus RCR tag

Csörúgós hömérö viselkedésének vizsgálata

_{Integráló tagok átmeneti függvényének megismerése}

_{Differenciáló tagok átmeneti függvényének megismerése}

Segédenergia nélküli gáznyomás szabályozó

Bode‑diagramok megismerése

Arányos tagok P1T, P2T

Integráló tagok idökésés mentes, I1T

Differenciáló tagok idökésés mentes, D1T

Stabilitás vizsgálata Bode‑diagramon

Átviteli tagok, -rendszerek leírása állapotváltozókkal és állapotegyenletekkel